
視線角與軌道攝動
如果地球站位於衛星正下方,則將接收最大訊號電平。否則,將無法接收最大訊號電平,並且隨著地球站經緯度差異的增加,訊號電平會降低。
因此,根據需求,我們可以將衛星放置在特定軌道上。現在,讓我們討論一下視線角。
視線角
地球站天線的以下兩個角度組合在一起稱為視線角。
- 方位角
- 仰角
通常,對於非地球同步軌道,這些角度的值會發生變化。而對於地球同步軌道,這些角度的值不會發生變化。因為,地球同步軌道上的衛星相對於地球看起來是靜止的。
這兩個角度有助於從地球站天線直接指向衛星。因此,地球站天線的最大增益可以指向衛星。
我們可以使用地球站的經度和緯度以及衛星軌道的方位來計算地球同步軌道的視線角。
方位角
地球站、衛星和地心所經過的平面與當地水平面之間的角度稱為方位角。
方位角 ($\alpha$) 的公式為
$$\alpha\: = 180^0 + Tan^{-1}\left(\frac{Tan G}{TanL}\right)$$
其中,
L 是地球站天線的緯度。
G 是衛星軌道位置與地球站天線位置之間的差值。
下圖顯示了方位角。
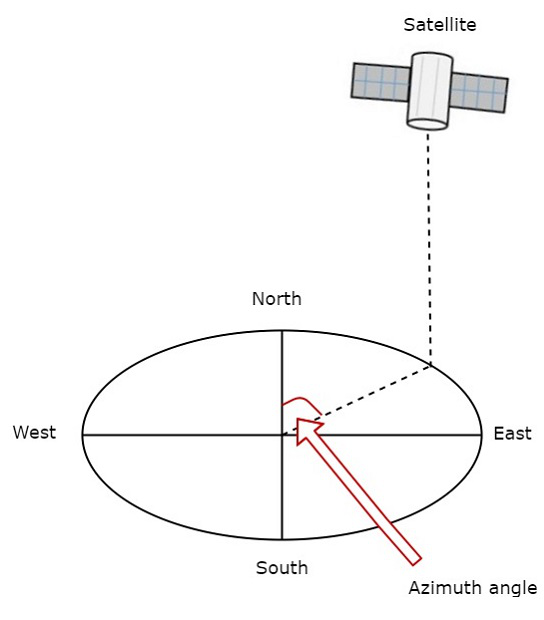
如圖所示,測量地球站天線到北極的水平角。它代表方位角。它用於水平跟蹤衛星。
仰角
指向衛星的直線與垂直平面之間的角度稱為仰角。垂直平面就是垂直於水平平面的平面。
仰角 ($\beta$) 的公式為
$$\beta = Tan^{-1}\left(\frac{cosG.cosL-0.15}{\sqrt{1-cos^2G.cos^2L}}\right)$$
我們可以使用上述公式計算仰角。下圖顯示了仰角。

如圖所示,測量地球站天線從地面到衛星的垂直角。它代表仰角。
軌道攝動
以下是由於引力和非引力作用或引數引起的軌道攝動。
由於質量分佈不均勻,地球周圍存在不規則的引力。地球磁場也導致軌道攝動。
主要的外部攝動來自太陽和月亮。當衛星靠近這些外部天體時,它會受到更強的引力。
低軌道衛星會受到與原子和離子碰撞引起的摩擦的影響。
太陽輻射壓力會影響使用大型太陽能電池陣列的大型地球同步軌道衛星。
天線發射的射頻輻射產生的自生扭矩和壓力。
大多數衛星使用推進子系統來維持適當的自旋軸方向並控制衛星對抗擾動力的高度。