衛星通訊 - 開普勒定律

我們知道衛星繞地球運轉，這類似於地球繞太陽運轉。因此，應用於地球及其繞太陽運動的原理也適用於衛星及其繞地球的運動。

許多科學家從早期就提出了不同型別的理論。但是，只有**約翰內斯·開普勒**(1571-1630)是最被認可的描述衛星繞地球運動原理的科學家之一。

開普勒提出了三個改變了整個衛星通訊理論和觀測的定律。這些定律被稱為**開普勒定律**。它們有助於視覺化太空中的運動。

開普勒第一定律

開普勒第一定律指出，衛星圍繞其中心天體（地球）執行的路徑將是**橢圓**。這個橢圓有兩個焦點 F1 和 F2，如下圖所示。地球的質心將始終位於橢圓的兩個焦點之一。

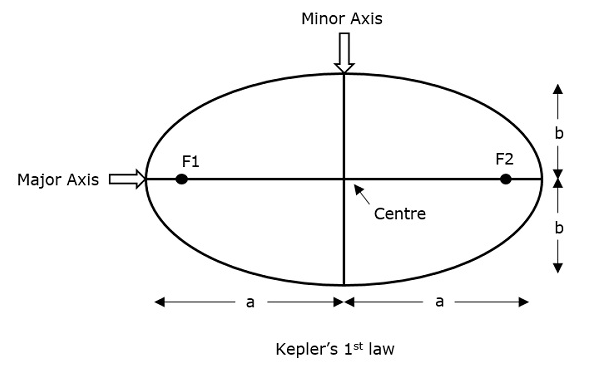
如果考慮從物體中心到其橢圓路徑上某一點的距離，那麼橢圓離中心最遠點稱為**遠地點**，橢圓離中心最近點稱為**近地點**。

該系統的**偏心率“e”**可以寫成：

$$e = \frac{\sqrt{a^2 - b^2}}{a}$$

其中，**a** 和 **b** 分別是橢圓長半軸和短半軸的長度。

對於**橢圓路徑**，偏心率 (e) 的值始終介於 0 和 1 之間，即 $0$ < $e$ < $1$，因為 a 大於 b。假設偏心率 (e) 的值為零，則路徑將不再是橢圓形，而是會變成圓形。

開普勒第二定律

開普勒第二定律指出，在相等的時間間隔內，衛星相對於地球質心所覆蓋的**面積**相同。這可以透過檢視下圖來理解。

假設衛星在相同的時間間隔內覆蓋了 p1 和 p2 的距離。那麼，衛星在這兩個時刻覆蓋的面積 B1 和 B2 相等。

開普勒第三定律

開普勒第三定律指出，橢圓軌道的週期時間的平方與長半軸長度的立方成正比。**數學表示式**如下：

$$T^2\:\alpha\:a^3$$

$$=> T^2=\left(\frac{4\pi ^2}{\mu }\right) a^3$$

其中，$\frac{4\pi^2}{\mu}$ 是比例常數。

$\mu$ 是開普勒常數，其值為 3.986005 x 10¹⁴m³ /sec²

$$1 = \left(\frac{2\pi}{T}\right)^2\left(\frac{a^3}{\mu}\right)$$

$$1 = n^2\left(\frac{a^3}{\mu}\right)$$

$$=> a^3 = \frac{\mu}{n^2}$$

其中，**‘n’** 是衛星的平均運動，單位為弧度每秒。

**注意** - 衛星繞地球運轉時，會受到來自地球的引力作用。類似地，它還會受到來自太陽和月球的引力作用。因此，衛星必須平衡這兩種力才能保持在軌道上。