SAS - Bland Altman 分析

Bland-Altman 分析是一種用於驗證兩種旨在測量相同引數的方法之間一致性或不一致性的過程。方法之間的高度相關性表明在資料分析中選擇了足夠好的樣本。在 SAS 中，我們透過計算變數值的平均值、上限和下限來建立 Bland-Altman 圖。然後我們使用 PROC SGPLOT 建立 Bland-Altman 圖。

語法

在 SAS 中應用 PROC SGPLOT 的基本語法如下：

PROC SGPLOT DATA = dataset;
SCATTER X = variable Y = Variable;
REFLINE value;

以下是所用引數的描述：

• 資料集是資料集的名稱。

• SCATTER 語句建立以 X 和 Y 形式提供的值的散點圖。

• REFLINE 建立水平或垂直參考線。

示例

在下面的示例中，我們採用兩種方法（名為 new 和 old）生成的兩個實驗的結果。我們計算變數值的差異，以及同一觀測值的變數的平均值。我們還計算標準差值，用於計算的上限和下限。

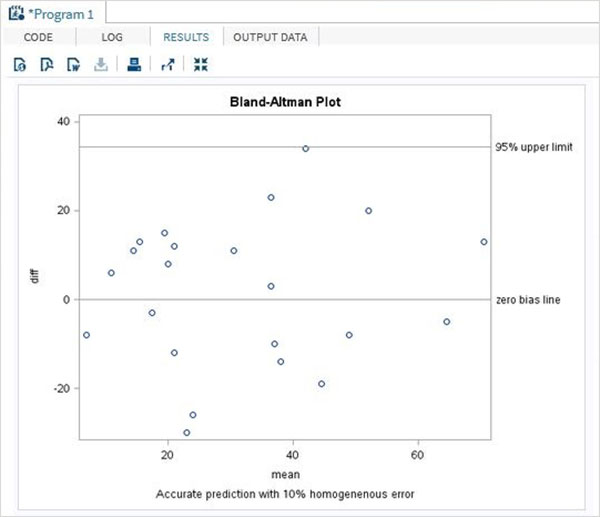
結果顯示 Bland-Altman 圖作為散點圖。

data mydata;
input new old;
datalines;
31 45
27 12
11 37
36 25
14 8
27 15
3 11
62 42
38 35
20 9
35 54
62 67
48 25
77 64
45 53
32 42
16 19
15 27
22 9
8 38
24 16
59 25
;

data diffs ;
set mydata ;
/* calculate the difference */
diff = new-old ;
/* calculate the average */
mean = (new+old)/2 ;
run ;
proc print data = diffs;
run;

proc sql noprint ;
select mean(diff)-2*std(diff),  mean(diff)+2*std(diff)
into   :lower,  :upper 
from diffs ;
quit;

proc sgplot data = diffs ;
scatter x = mean y = diff;
refline 0 &upper &lower / LABEL = ("zero bias line" "95% upper limit" "95%
lower limit");
TITLE 'Bland-Altman Plot';
footnote 'Accurate prediction with 10% homogeneous error'; 
run ;
quit ;

執行上述程式碼後，將得到以下結果：

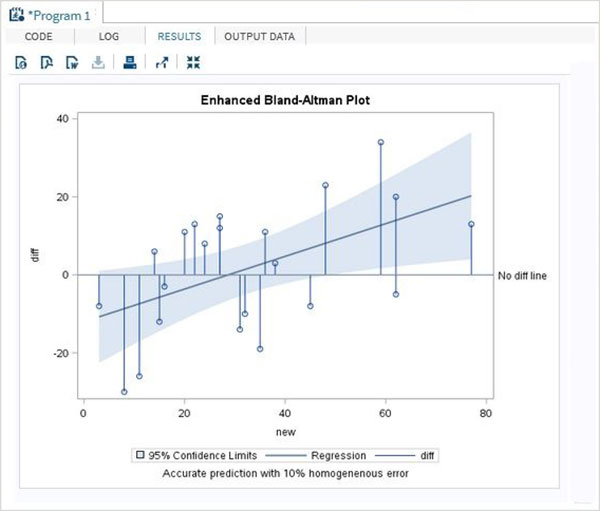
增強模型

在上述程式的增強模型中，我們得到了 95% 的置信水平曲線擬合。

proc sgplot data = diffs ;
reg x = new y = diff/clm clmtransparency = .5;
needle x = new y = diff/baseline = 0;
refline 0 / LABEL = ('No diff line');
TITLE 'Enhanced Bland-Altman Plot';
footnote 'Accurate prediction with 10% homogeneous error'; 
run ;
quit ;

執行上述程式碼後，將得到以下結果：