資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究串聯電阻
當電阻器首尾相連，電流只有一條路徑可流過時，這些電阻器就被稱為串聯連線。
解釋
假設三個純電阻R1、R2和R3串聯連線到一個直流電壓源V上，電路圖如下所示。
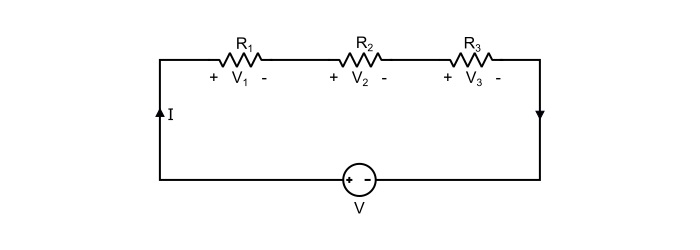
參考電路圖，可以寫成
$$\mathrm{\mathit{V}\:=\:\mathit{V}_{1}+\mathit{V}_{2}+\mathit{V}_{3}\:\:\:\:…(1)}$$
其中V1、V2和V3分別是各個電阻器上的電壓降。
假設I為電路中的總電流，R為所有串聯電阻的等效電阻。因此，方程(1)可以寫成
$$\mathrm{\mathit{IR}=\mathit{IR}_{1}+\mathit{IR}_{2}+\mathit{IR}_{3}}$$
$$\mathrm{\Rightarrow\:\mathit{R}=\mathit{R}_{1}+\mathit{R}_{2}+\mathit{R}_{3}\:\:\:\:…(2)}$$
因此，方程(2)證明了“串聯連線電阻的等效電阻等於各個電阻之和”。
串聯連線電阻的總功率損耗由下式給出
$$\mathrm{\mathit{P}=\mathit{I}^{2}\mathit{R}_{1}+I^{2}\mathit{R}_{2}+I^{2}\mathit{R}_{3}}$$
$$\mathrm{\Rightarrow\:\mathit{P}=\mathit{I}^{2}(\mathit{R}_{1}+\mathit{R}_{2}+\mathit{R}_{3})=\mathit{I}(\mathit{V}_{1}+\mathit{V}_{2}+\mathit{V}_{3})}\:\:\:\:…(3)$$
關於串聯電阻的重要說明
串聯電阻的總電阻等於各個電阻之和。
每個電阻中的電流相同。
串聯電阻的總電阻或等效電阻大於最大電阻值。
串聯電阻的總功耗等於各個電阻功耗之和。
數值示例 (1)
確定電路的等效電阻。另外，求出電路的總電流和總功率損耗。
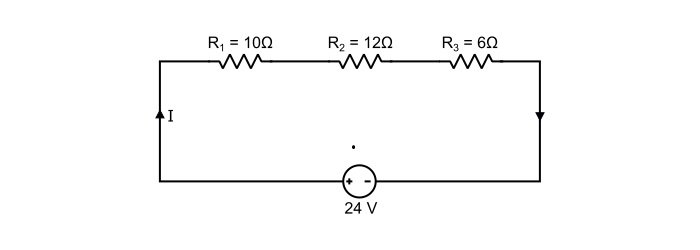
解答
由於電阻器是串聯連線的，因此
$$\mathrm{\mathit{R}_{eq}=\mathit{R}_{1}+\mathit{R}_{2}+\mathit{R}_{3}}$$
$$\mathrm{\Rightarrow\:\mathit{R}_{eq}=10+12+6=28 \:Ω}$$
總電路電流為
$$\mathrm{\mathit{I}=\frac{\mathit{V}}{\mathit{R}_{eq}}=\frac{24}{28}=0.857\:A}$$
電路的總功率損耗為
$$\mathrm{\mathit{P}=\mathit{I}^{2}\mathit{R}_{eq}=0.857^{2}×28=20.565 \:W}$$
數值示例 -2
一個200瓦的電燈泡的燈絲設計用於110伏的電源。需要串聯連線一個多大的電阻，才能使燈泡在230伏的電源下工作？
解答
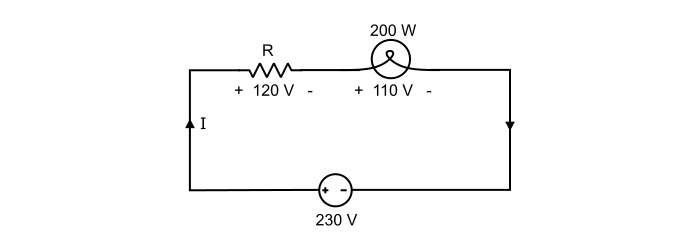
參考電路圖，
$$\mathrm{燈泡的額定電流,\mathit{I}=\frac{\mathit{P}}{\mathit{V}}=\frac{200}{110}=1.82 A}$$
如果R歐姆是需要與燈泡串聯的電阻值，則
$$\mathrm{串聯電阻上的電壓降\:\mathit{V}_{R}=230−110=120\:V}$$
因此，
$$\mathrm{\mathit{R}=\frac{\mathit{V}_{R}}{\mathit{I}}=\frac{120}{1.82}=65.93\:Ω}$$
瀏覽量：341
