資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究(a) 兩個燈泡，分別標註為100 W，220 V和10 W，220 V，並聯連線到220 V電源。計算電路中的總電流。(b) 兩個電阻X和Y，阻值分別為2Ω和3Ω，先並聯連線，再串聯連線。兩種情況下，電源電壓均為5 V。(i) 繪製電路圖以顯示每種情況下電阻的組合。(ii) 計算電阻串聯組合中3Ω電阻兩端的電壓。
(a) 已知
第一個燈泡的功率，$P_1$ = 100W，第一個燈泡的電壓，$V_1$ = 220V
第二個燈泡的功率，$P_2$ = 10W，第二個燈泡的電壓，$V_2$ = 220V
求解：電路中的總電流，$I$。
解答
兩個燈泡兩端的電壓相同，均為220V。
我們知道，
$P=V\times I$，其中 P = 功率，V = 電壓，I = 電流。
根據電流 $I$，可以表示為：
$I=\frac{P}{V}$
現在，
將燈泡的已知值代入上式，我們得到：
100W燈泡的電流 = $I_1=\frac{{P}_{1}}{V}$ = $\frac{100}{220}A$
10W燈泡的電流 = $I_2=\frac{{P}_{2}}{V}$ = $\frac{10}{220}A$
因此，電路中的總電流為
$I=I_1+I_2$
$I=\frac{100}{220}+\frac{10}{220}$
$I=\frac{100+10}{220}$
$I=\frac{110}{220}$
$I=0.5A$
(b) (i) 每種情況下電阻組合的電路圖
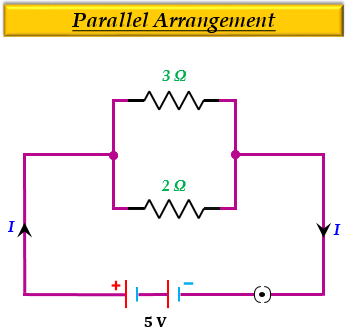
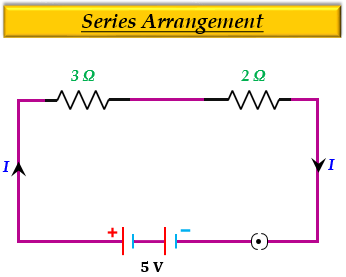
(ii) 已知
X 的電阻 = $R_1$ = $2\Omega$
電壓，$V$ = 6V (原文此處應為5V，此處已更正)
求解：串聯電阻組合中3Ω電阻兩端的電壓。
解答
我們知道，串聯組合中的等效電阻（或總電阻）為
$R_{eq}=R_1+R_2$
代入 $R_1$ 和 $R_2$ 的值，我們得到：
$R_{eq}=2+3$
$R_{eq}=5\Omega$
我們知道電流為：
$I=\frac {V}{R}$
這裡，
$I=\frac {V}{R_{eq}}$
所以，代入已知值，我們得到：
$I=\frac {5}{5}$
$I=1A$
因此，電路中的電流為1A。
現在，
為了找到3Ω電阻兩端的電壓，我們使用電壓公式：
$V=I\times {R}$
代入所需的值，我們得到：
$V=1\times {3}$
$V=3V$
因此，3Ω電阻兩端的電壓為3伏特。
128 次檢視
