資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學交流電路中的電阻
重要術語
交流電路 − 交流電流所遵循的閉合路徑稱為交流電路。
電阻 − 材料在電流路徑中提供的阻礙程度稱為該材料的電阻。具有電阻的元件稱為電阻器。
電壓或電流峰值 − 交流量達到的最大值。也稱為幅度。
平均值 − 一個週期內所有交流量值的算術平均值稱為平均值。對於正弦電壓或電流，
$$\mathrm{I_{avg}=\frac{2I_{m}}{\pi}=0.637I_{m}}$$
$$\mathrm{V_{avg}=\frac{2V_{m}}{\pi}=0.637I_{m}}$$
均方根 (RMS) 值 − 交流電流的RMS值是指在給定時間內流過給定電阻時產生與交流電流在相同電阻和相同時間內產生的熱量相同的直流電流值。正弦電流和電壓的RMS值是：
$$\mathrm{I_{RMS}=\frac{I_{m}}{\sqrt{2}}=0.707I_{m}}$$
$$\mathrm{V_{RMS}=\frac{V_{m}}{\sqrt{2}}=0.707V_{m}}$$
瞬時功率 (p) − 它是電阻上的瞬時電壓(v)與流過電阻的瞬時電流(i)的乘積。
瞬時功率值可能是正值或負值。正值表示功率從電源流向負載。負值表示功率從負載流向電源。
$$\mathrm{瞬時功率\:(p)=\upsilon i=\frac{V_{m}I_{m}}{2}-\frac{V_{m}I_{m}}{2}cos(2 \omega t)\:\:\:(瓦)}$$
平均功率 (P) − 平均功率是一個週期內瞬時功率的平均值。
$\mathrm{平均功率\:(p)= (p=}$
$\upsilon i)在一個週期內的平均值=\frac{V_{m}I_{m}}{2}=VI\:\:(瓦)$
$$\mathrm{V=施加電壓的RMS值}$$
$$\mathrm{I=電路電流的RMS值}$$
包含電阻的交流電路
考慮一個電路，其中包含一個純電阻R Ω 歐姆，連線到交流電壓源。
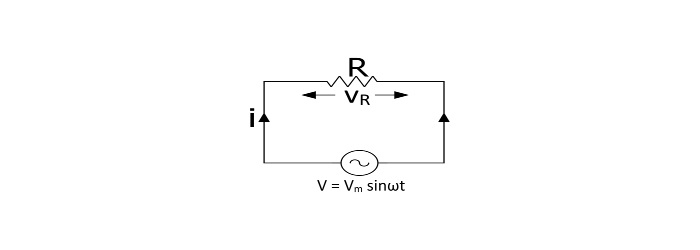
設交流電壓由以下方程給出：
$$\mathrm{
u=V_{m}sin\:\omega t} ...(1)$$
由於該電壓，交流電流i將流過電路。整個施加電壓僅出現在電阻兩端。因此，
$$\mathrm{
u=iR}$$
$$\mathrm{i=\frac{
u}{R}=\frac {v_{m}\:sin\:\omega t }{R}=I_{m}\:sin\:\omega t.....(2)}$$
$$其中，\mathrm{I_{m}=\frac{V_{m}}{R}=電路電流的最大值}$$
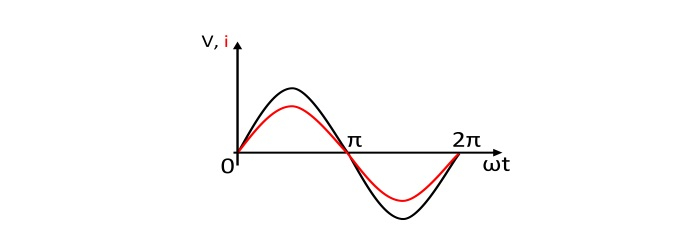
從公式(1)和(2)可以看出，流過純電阻的電流與電阻兩端的電壓同相。
電阻電路中的功率
- 瞬時功率
$$\mathrm{p=
u i=\frac{V_{m}I_{m}}{2}-\frac{V_{m}I_{m}}{2}cos(2 \omega t)}$$
瞬時功率由兩部分組成，即一個常數部分 (VmIm/2) 和一個波動部分 (VmIm/2)cos 2ωt。
- 平均功率
$$\mathrm{平均功率\:(p)= (p=}$
$\upsilon i)在一個週期內的平均值=\frac{V_{m}I_{m}}{2}=VI}$$
相量圖和波形圖
- 相量圖
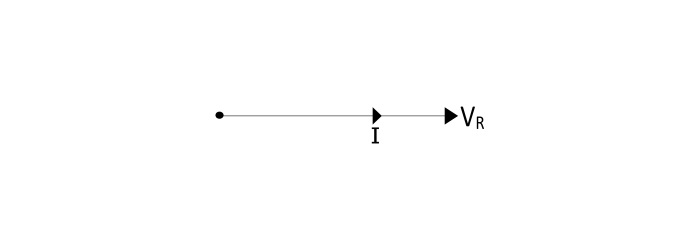
- 電流和電壓波形圖
- 功率曲線
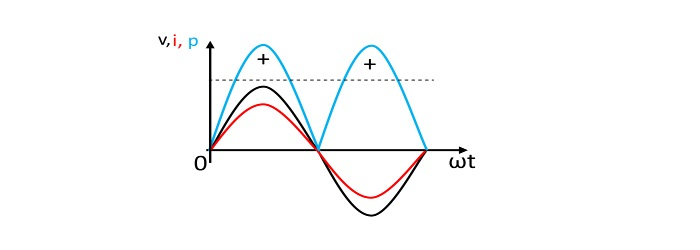
數值例子
一個交流電路包含一個20Ω的純電阻，並連線到一個240V、50Hz的交流電源。計算(i)電路電流 (ii)電阻消耗的功率和 (iii)電壓和電流的方程。
解答
- 電路電流
$$\mathrm{I=\frac{V}{R}=\frac{240}{20}=12A}$$
- 電路消耗的功率
$$\mathrm{P=VI=240×12=2880\:W}$$
- 電壓和電流的方程
$$\mathrm{V_{m}=\sqrt{2}V=\sqrt{2}×240=339.36\:V}$$
$$\mathrm{I_{m}=\sqrt{2}I=\sqrt{2}×12=16.97 A}$$
$$\mathrm{\omega=2\pi f=2\pi×50=314\:rad/sec}$$
因此，
$$\mathrm{
u=339.36sin(314t)\:\:\:V}$$
$$\mathrm{i=16.97sin(314t)\:\:\:A}$$
1K+ 次瀏覽
