資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律學交流電路中的電感器
考慮包含一個純電感線圈（電感為 L 亨利）的電路。當一個交流電壓 V（RMS）施加線上圈兩端時，一個交流電流 I（RMS）將流過電路。由於這個交流電流，線上圈中會由於其電感而產生一個反電動勢 (e)。這個反電動勢在每個時刻都阻礙電流透過線圈的變化。
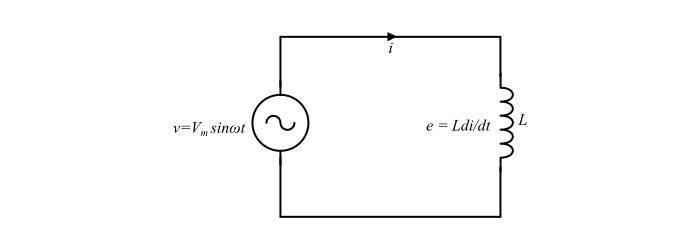
假設施加的交流電壓為
$$\mathrm{
u=V_{m}sin\:\omega t}\:\:\:… (1)$$
電感器線圈中產生的反電動勢 (e) 由下式給出：
$$\mathrm{e=L \frac{di}{dt}}\:\:\:… (2)$$
由於沒有歐姆壓降，因此施加的電壓只需要克服反電動勢即可。因此，
施加電壓 = 反電動勢
$$\mathrm{V_{m}\:sin\:\omega t =L \frac{di}{dt}}$$
$$\mathrm{di=\frac{V_{m}}{L}sin\: \omega t dt}$$
對兩邊進行積分，得到：
$$\mathrm{i=\frac{V_{m}}{L}\:\int \:sin\:\omega t\:dt=\frac{V_{m}}{L}(\frac{-cos\:\omega t}{\omega})=\frac{V_{m}}{\omega\:L}(-cos\:\omega t)}$$
$$\mathrm{\Rightarrow\:i=\frac{V_{m}}{\omega\:L}sin(\omega t-90^{\circ})}\:\:\:… (3)$$
在公式 (3) 中，當 sin (ωt - 90°) = 1 時，i 的值將最大。因此，
$$\mathrm{I_{m}=\frac{V_{m}}{\omega\:L}}\:\:\:… (4)$$
因此，公式 (3) 變為：
$$\mathrm{i=I_{m}sin(\omega t-90^{\circ})}\:\:\:… (5)$$
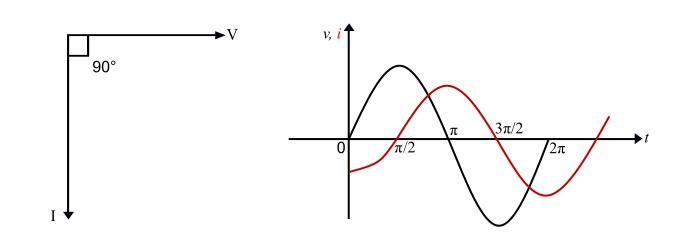
從公式 (5) 可以看出，純電感上的電流滯後於電感上的電壓 90°。它也可以用相量圖和波形表示為：
感抗
由於我們已經看到
$$\mathrm{I_{m}=\frac{V_{m}}{\omega\:L}}$$
$$\mathrm{\Rightarrow\:\frac{V_{m}}{I_{m}}=\omega\:L=X_{L}}$$
$$\mathrm{\Rightarrow\:X_{L}=\omega\:L=2\pi\:fL=\frac{V_{m}/ \sqrt{2}}{I_{m}\sqrt{2}}=\frac{V}{I}}\:\:\:… (6)$$
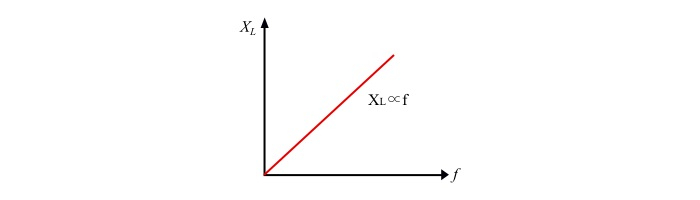
其中，V 和 I 分別是電壓和電流的 RMS 值。ω = 2πfL 是角供電頻率。
因此，XL 是電感器對電流流動的阻抗。它被稱為電感線圈的感抗。XL 的單位為歐姆 (Ω)。
功率
**瞬時功率** - 瞬時功率 (p) 由瞬時電壓和瞬時電流的乘積給出，如下所示：
$$\mathrm{p=
u×i=V_{m}sin \:\omega\:t×I_{m}sin(\omega\:t-90^{\circ})=-V_{m}I_{m}sin\:\omega t\:cos\:\omega t}$$
$$\mathrm{\Rightarrow\:p=-\frac{V_{m}\:I_{m}}{2}sin\:2\omega t}\:\:\:… (7)$$
**平均功率** - 平均功率 (P) 是一個週期內瞬時功率的平均值。因此，
$$\mathrm{p=\frac{1}{2\pi}\int_{0}^{2\pi}-\frac{V_{m}\:I_{m}}{2}sin\:2\omega t\:d\omega t}\:\:\:… (8)$$
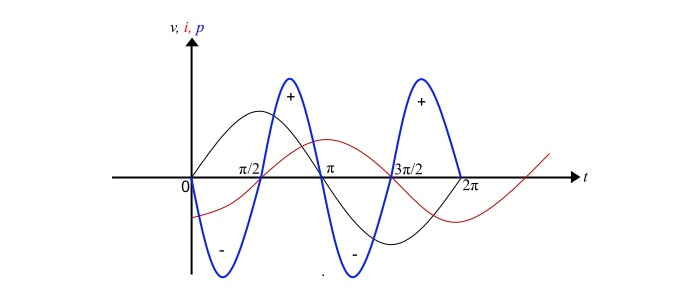
因此，純電感在一個週期內吸收的平均功率為零。功率曲線在一個週期內顯示正功率等於負功率。因此，在一個週期內的合成功率為零，即電感沒有消耗功率。電功率僅在電源和線圈之間來回流動。
數值示例
當一個純電感線圈連線到一個 250 V，50 Hz 的電源上時，透過它的電流為 20 A。確定以下內容：
- 感抗
- 線圈的電感
- 吸收功率
- 電壓和電流的方程式。
解決方案
- 感抗
$$\mathrm{X_{L}=\frac{V}{I}=\frac{250}{20}= 12.5 Ω}$$
- 線圈的電感
$$\mathrm{∵X_{L}=2\pi fL}$$
$$\mathrm{\Rightarrow L=\frac{X_{L}}{2\pi f}=\frac{12.5}{2\pi×50}=0.0398 H = 39.8 mH}$$
- 吸收功率 - 由於給定的線圈是純電感。因此，**吸收功率為零**。
- 電壓和電流的方程式
$$\mathrm{電壓的最大值，V_{m}=√2 × V=√2 × 250 = 353.5 V}$$
$$\mathrm{電流的最大值，I_{m}=\frac{V_{m}}{X_{L}}=\frac{353.5}{12.5}= 28.28 A}$$
$$\mathrm{角頻率，ω=2\pi f=2\pi× 50 = 314 rad⁄sec}$$
因此，
$$\mathrm{電壓方程式，
u= 353.5\:sin 314t}$$
$$\mathrm{電流方程式，t= 28.28\:sin(314t− 90^{\circ})}$$
2K+ 次檢視
