資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究串聯電感（有無互感）
當兩個電感器首尾相連，即一個電感器的末端連線到另一個電感器的起始端，並且相同的電流流過這兩個電感器時，則稱這兩個電感器串聯連線。
無互感串聯電感
考慮兩個電感，電感分別為 $L_{1}$ 和 $L_{2}$，串聯連線（見圖）。假設兩個線圈之間的互感為零。設 $L_{T}$ 為串聯電感的總等效電感。
假設在任意時刻，電流以 di/dt 的速率變化。電路中的總感應電動勢等於 $L_{1}$ 和 $L_{2}$ 中感應電動勢的總和。
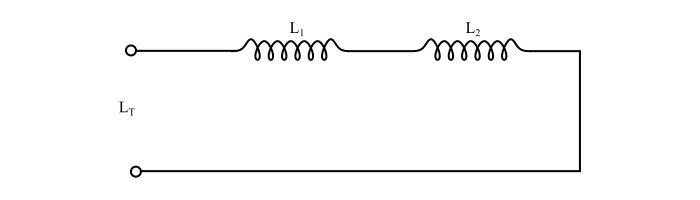
參考圖示，我們有：
$$\mathrm{e=L_{1}\frac{di}{dt}+L_{2}\frac{di}{dt}}$$
$$\mathrm{\Longrightarrow e=(L_{1}+L_{2})\frac{di}{dt}}$$
同時，
$$\mathrm{e=L_{T}\frac{di}{dt}}$$
因此，
$$\mathrm{L_{T}=L_{1}+L_{2}}$$
類似地，對於 n 個串聯電感，等效電感將為
$$\mathrm{L_{T}=L_{1}+L_{2}+L_{3}+......+L_{n}}$$
有互感串聯電感
考慮兩個串聯連線的電感。設
$$\mathrm{L_{1} = 第一個電感的電感}$$
$$\mathrm{L{2} = 第二個電感的電感}$$
M = 電感器之間的互感
情況 1 - 串聯互助連線 在這種情況下，兩個電感器連線在一起，使得它們的磁通相互增強，即方向相同。假設在任意時刻，電流的變化率為 di/dt。總感應電動勢將等於 $L_{1}$ 和 $L_{2}$ 中感應電動勢的總和以及互感電動勢。
參考圖示，我們得到：
$$\mathrm{e=L_{1}\frac{di}{dt}+L_{2}\frac{di}{dt}+M\frac{di}{dt}+M\frac{di}{dt}}$$
$$\mathrm{\Longrightarrow e=(L_{1}+L_{2}+2M)\frac{di}{dt}}$$
如果 $L_{T}$ 為電路的總電感，則
$$\mathrm{e=L_{1}\frac{di}{dt}}$$
因此，
$$\mathrm{L_{T}=L_{1}+L_{2}+2M}$$
這裡，磁通量是互助的。
情況 2 - 串聯對置連線 在這種情況下，兩個電感器連線在一起，使得它們的磁通相互抵消，即方向相反。假設在任意時刻，電流的變化率為 di/dt。電路中的總感應電動勢將等於 $L_{1}$ 和 $L_{2}$ 中感應電動勢的總和減去互感電動勢。
參考圖示，我們得到：
$$\mathrm{e=L_{1}\frac{di}{dt}+L_{2}\frac{di}{dt}-M\frac{di}{dt}-M\frac{di}{dt}}$$
$$\mathrm{\Longrightarrow e=(L_{1}+L_{2}-2M)\frac{di}{dt}}$$
如果 $L_{T}$ 為電路的電感，則
$$\mathrm{e=L_{1}\frac{di}{dt}}$$
因此，
$$\mathrm{L_{T}=L_{1}+L_{2}-2M}$$
這裡，磁通量是減性的。
2K+ 次瀏覽
