關係與函式練習題

---

引言

關係和函式是兩個集合之間的對映。關係和函式的應用存在於現實世界的每一個角落。

在數學科學中，關係和函式是相互關聯的研究課題。

例如，將基本單位從米轉換為釐米，人的身高和體重，不同氣候條件下的體溫，員工工作的年收入等。

如果一個輸入只有一個輸出，則該關係是一個函式。有序對中輸入和輸出的關係是一個關係。

關係和函式練習題將提供對概念的基本理解，並幫助他們瞭解其在現實世界中的應用。

什麼是關係？

• 兩個或多個非空集合的有序對中的輸入值和輸出值是關係。

• 它是所提供的非空集合的集合元素之間的連線或關係。

例如，

兩個非空集合 $\mathrm{A\:=\:\lbrace\:d\:,\:g\:,\:k\:,\:m\:\rbrace}$ 和 $\mathrm{B\:=\:\lbrace\:a\:,\:s\:,\:h\:,\:b\:\rbrace}$ 的關係由 $\mathrm{R\:=\:\lbrace\:(d\:,\:a)\:,\:(g\:,\:s)\:,\:(k\:,\:h)\:,\:(m\:,\:b)\:,\:(g\:,\:h)\rbrace}$ 給出

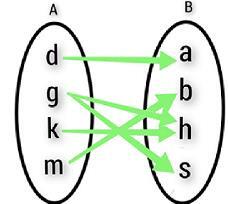
從這個對映中，我們一致認為關係並非在所有情況下都是函式。

給定的例子是一個關係，但不是一個函式，因為它對相同的輸入有多個輸出值。

關係有哪些型別？

關係有不同的型別，即空關係、自反關係、傳遞關係、對稱關係、逆關係、恆等關係、全域關係和等價關係。

空關係

如果一個集合的輸入值與另一個集合的值之間沒有對映，則稱為空關係或無效關係。

$$\mathrm{R\:=\:\phi}$$

自反關係

如果集合 A 的元素對映到自身，則該關係稱為自反關係。

傳遞關係

如果 $\mathrm{pRq\:and\:qRr\:\Longrightarrow\:pRr}$，則稱關係為傳遞關係。

對稱關係

對稱關係包含一個集合的有序對及其反向有序對。

逆關係

如果一個集合包含另一個集合的逆對，則這種型別的關係稱為逆關係。

恆等關係

如果集合 A 中的所有元素都對映到自身，則稱關係為恆等關係。

全域關係

如果一個集合的所有元素都對映到另一個集合的元素或集合本身，則這種型別的關係稱為全域關係。

等價關係

如果一個關係是對稱的、傳遞的和自反的，我們稱該關係為等價關係。

什麼是函式？

在關係中，如果每個輸入值都分配給一個不同的輸出值，則該關係稱為函式。

• 函式的定義域是函式所有輸入的集合。

• 函式的陪域是可能成為函式輸出的元素的集合。

• 函式的值域是函式的輸出值。

例如

令兩個非空集合為 {2, 3, 5} 和 {3, 4, 6, 7, 8}。如果關係 𝑅 ={(2, 3), (3, 4), (5, 6)}。定義域、陪域和值域是什麼？

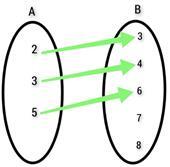
答案 -

函式的定義域 = {2, 3, 5}

函式的陪域 = {3, 4, 6, 7, 8}

函式的值域 = {3, 4, 6}

函式有哪些型別？

對映有各種型別，即一對一函式、滿射函式和入射函式。

一對一函式

如果每個輸入值都有一個不同的輸出值，則這種型別的函式稱為一對一函式。

滿射函式

如果每個輸出值在另一個集合中都存在一個值，則稱為滿射函式或滿射。

入射函式

如果陪域集合中至少有一個元素沒有被定義域集合的任何元素對映，則稱該函式為入射函式。

例題解析

1) 令 $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ 為由 $\mathrm{f(x)\:=\:x^{2}\:+\:1}$ 定義的函式，其中 𝒙 取值 0、1、2 和 3。求函式的值域。

答案 -

將給定的輸入值代入 $\mathrm{f(x)\:=\:x^{2}\:+\:1}$，得到

$\mathrm{f(0)\:=\:1\:,\:f(1)\:=\:2\:,\:f(2)\:=\:5\:and\:f(3)\:=\:10}$

函式的值域 = {1, 2, 5, 10}

2) 從給定的對映圖中，求函式的定義域和值域。

答案 -

定義域 $\mathrm{=\:\lbrace\:Fire\:,\:Water\:,\:Land\:,\:Wind\:\rbrace}$

值域 $\mathrm{=\:\lbrace\:Wood\:,\:Breeze\:,\:Sand\:,\:Fish\:\rbrace}$

3) 令兩個非空集合為 $\mathrm{A\:=\:\lbrace\:7\:,\:8\:,\:9\:,\:10\:\rbrace}$ 和 $\mathrm{B\:=\:\lbrace\:1\:,\:2\:,\:3\:,\:4\:\rbrace}$。如果從 A 到 B 定義了一個函式 $\mathrm{f(x)}$，那麼函式的輸入值和輸出值是什麼？

答案 -

輸入值將是集合 $\mathrm{A\:=\:\lbrace\:7\:,\:8\:,\:9\:,\:10\:\rbrace}$

輸出值將是集合 $\mathrm{B\:=\:\lbrace\:1\:,\:2\:,\:3\:,\:4\:\rbrace}$

4) 從給定的對映圖中，求函式的定義域、陪域和值域。

答案 -

定義域 = {2,4,6,8,10}

陪域 = {1,3,5,7,9}

值域 = {1, 9}

5) 從 A 到 B 的函式 F 定義為 $\mathrm{\lbrace\:(1\:,\:b)\:,\:(3\:,\:e)\:,\:(7\:,\:m)\:,\:(9\:,\:u)\:\rbrace}$。繪製該函式的對映圖並說明其型別。

答案 -

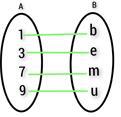
上述對映是一對一函式。

6) 令 $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ 為一個函式，使得 $\mathrm{f(x)\:=\:\lbrace\:(4\:,\:6)\:,\:(7\:,\:9)\:,\:(8\:,\:9)\:\rbrace}$。藉助對映圖找出函式的型別。

答案 -

給定函式的型別是滿射。

7) 如果函式的定義域為 {𝟐, 𝟓, 𝟗}，值域為 {𝟐, 𝟓, 𝟗}。這種型別的關係叫什麼，它是一個函式嗎？

答案 - 如果每個元素都與其自身相關，則該關係是自反的。是的，這種型別的關係是一個函式。

8) 假設函式由 $\mathrm{f(x)\:=\:\lbrace\:(1\:,\:1)\:,\:(2\:,\:2)\:,\:(3\:,\:3)\:,\:(4\:,\:4)\:\rbrace}$ 定義。該函式是什麼型別的關係？

答案 -

在給定的函式中

$\mathrm{f(x)\:=\:\lbrace\:(1\:,\:1)\:,\:(2\:,\:2)\:,\:(3\:,\:3)\:,\:(4\:,\:4)\:\rbrace}$，關係的型別是恆等關係。因為集合中的所有元素都對映到自身。

9) 如果函式的值域為 $\mathrm{\lbrace\:e\:,\:r\:,\:f\:,\:g\:,\:h\:\rbrace}$。定義的函式是什麼？

答案 - 給定的資料不足。在不知道定義域的情況下，給定的值域將無效，並且無法確定關係或函式的型別。

10) 如果集合 $\mathrm{A\:=\:\lbrace\:W\:,\:X\:,\:Y\:,\:Z\:\rbrace}$ 和集合 $\mathrm{B\:=\:\lbrace\:A\:,\:B\:,\:C\:,\:D\:\rbrace}$，並且從 A 到 B 的定義函式 F 為 $\mathrm{f(x)\:=\:\lbrace\:(W\:,\:C)\:,\:(X\:,\:D)\:,\:(Y\:,\:B)\:,\:(Z\:,\:A)\:\rbrace}$。對映給定的函式。

答案 -

11) 從給定的對映圖中，求從 A 到 B 的定義函式 F。

答案 - 從 A 到 B 定義的函式為 {(1,2), (2,4), (3,5), (4,6)}

12) 從給定的對映圖中，求非空集合。

解 - 非空集合為 $\mathrm{A\:=\:\lbrace\:a\:,\:b\:,\:c\:\rbrace}$ 和 $\mathrm{B\:=\:\lbrace\:11\:,\:22\:,\:44\:\rbrace}$

練習題

• 假設函式由 $\mathrm{f(x)\:=\:\lbrace\:(a\:,\:a)\:,\:(b\:,\:b)\:,\:(c\:,\:c)\:,\:(d\:,\:a)\:\rbrace}$ 定義。該函式是什麼型別的關係？

• 令 $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ 為由 $\mathrm{f(x)\:=\:2x^{3}\:+\:1}$ 定義的函式，其中 𝑥 取值 1、2、3 和 4。求函式的值域。

• 從 A 到 B 的函式 F 定義為 $\mathrm{\lbrace\:(F\:,\:D)\:,\:(Y\:,\:D)\:,\:(U\:,\:P)\:,\:(S\:,\:Q)\:\rbrace}$。繪製該函式的對映圖並說明其型別。

• 從給定的對映圖中，求從 A 到 B 的定義函式 F。

• 令 $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ 為由 $\mathrm{f(x)\:=\:x\:+\:5}$ 定義的函式，對於每個 𝑥 > 0，繪製定義函式的對映圖。

• 如果關係由 $\mathrm{R\:=\:\lbrace\:(9\:,\:0)\:,\:(2\:,\:5)\:,\:(7\:,\:8)\:,\:(7\:,\:4)\:\rbrace}$ 定義。R 是函式嗎？

• 如果函式 $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ 由 𝑓(𝑥) = {(e,p), (l,b), (s,f),(k,q)} 定義。求函式的定義域和值域。

結論

• 關係是一組有序對，定義了兩個或多個集合的元素之間的連線。

• 函式是一種關係，其中每個輸入都有唯一的輸出。

• 輸入值是函式的定義域。

• 值域是陪域的一部分或子集。

• 為了找到函式的型別，我們應該將值從定義域對映到陪域。

常見問題

1. 函式中的原像和像是什麼？

• 對映到給定元素集的元素集稱為原像。它是陪域的一個子集。

• 函式可能產生的所有輸出值的集合稱為函式的像。它是定義域的一個子集。

2. 什麼時候關係不是函式？

如果單個輸入值有兩個或多個輸出，則這種型別的一對多對映不是函式。

例如 $\mathrm{R\:=\:\lbrace\:(a\:,\:n)\:,\:(e\:,\:t)\:,\:(a\:,\:v)\:,\:(m\:,\:g)\rbrace}$

3. 什麼是垂直線檢驗？

如果函式的曲線與我們在 XY 平面上繪製的垂直線相交不止一次，則它不是函式，但如果垂直線與一個點相交，則它是一個函式。這是確定函式是否只有一個輸出值或多個輸出值的視覺化方法之一。

4. 什麼是雙射函式？

如果一個函式是一對一的且是滿射的，則稱該函式為雙射函式。

5. 什麼型別的函式被稱為單射函式？

如果一個函式是一對一的，那麼這個函式就被稱為單射函式。