關係與函式

---

介紹

關係定義為一個元素對另一個元素的相互依賴。在數學中，函式表示兩組元素之間的特定關係。在本教程中，我們將討論關係和函式的含義、它們的各種型別以及函式的反函式，並附帶已解決的示例。

關係

關係是兩個類或集合之間的二元關係，表示這兩個類的元素以某種方式相關。兩個集合X和Y之間的二元關係是一組有序元素對，即(x, y)，使得元素x屬於集合X，元素y屬於集合Y。關係用符號R表示。它包含兩組元素的有序對。

數學上，二元關係可以表示為

$$\mathrm{X\:\times\:Y\:=\:=\:\lbrace(x\:,\:y)\:\lvert\:x\:\varepsilon\:X\:and\:y\:\varepsilon\:Y\rbrace}$$

這裡X被稱為R的定義域，Y被稱為R的值域。數學中的關係可以用三種方式表示。

• 列舉法 - 在這種表示方法中，關係通常以元素的有序對的形式表示。

例如，$\mathrm{set\:A\:=\:\lbrace\:-1\:,\:4\:,\:0\:,\:8\:\rbrace\:,\:B\:=\:\lbrace\:-2\:,\:-11\:,\:4\:,\:-2\:\rbrace}$

現在，兩組之間的關係可以表示為

$\mathrm{R\:\colon\:A\:\rightarrow\:B\:=\:\lbrace\:(-1\:,\:-2)\:,\:(4\:,\:-11)\:,\:(0\:,\:4)\:,\:(8\:-2)\rbrace\:}$

• 集合構造器法 - 這用於以簡短的形式表達大量元素。它用於藉助方程或區間來描述集合之間的關係。

例如，$\mathrm{\lbrace\:3\:,\:6\:,\:9\:,\:12\:,\:15\:,\:18\:,\:21\:\rbrace\:}$

現在，它可以表示為

$\mathrm{\lbrace\:p\:\colon\:p\:=\:3n\:,\:n\:\varepsilon\:N\:,\:1\:\leq\:n\:\leq\:7\:\rbrace\:}$

• 箭頭圖 - 在這種方法中，一組個體元素與另一組個體元素之間的關係透過繪製從左到右的箭頭來表示。

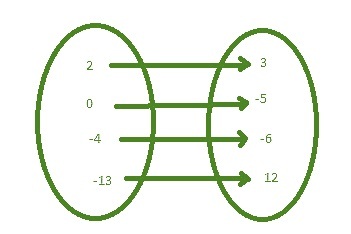
例如 - $\mathrm{set\:A\:=\:\lbrace\:2\:,\:0\:,\:-4\:,\:-13\:\rbrace\:,\:B\:=\:3\:,\:-5\:,\:-6\:,\:12\:\rbrace\:}$

現在，兩組之間的關係可以表示為

$\mathrm{R\:\colon\:A\:\rightarrow\:B\:=\:\lbrace\:(2\:,\:3)\:,\:(0\:,\:-5)\:,\:(-4\:,\:-6)\:,\:(-13\:,\:12)\:\rbrace\:}$

關係的型別

在數學中，使用了各種型別的關係。下面簡要介紹每種型別的關係。

• 自反的

• 對稱的

• 傳遞的

• 等價的

讓我們詳細討論每種型別的關係。

自反的

如果$\mathrm{(p\:,\:p)\:\varepsilon\:R\:,\:for\:every\:p\:\varepsilon\:A}$，則R被稱為自反的。

對稱的

當且僅當$\mathrm{(p\:,\:q\:)\:\varepsilon\:R\:,\:then\:(q\:,\:p)\:\varepsilon\:R}$時，R被稱為對稱的。

傳遞的

當且僅當$\mathrm{(p\:,\:q\:)\varepsilon\:R\:and\:(q\:,\:r)\varepsilon\:R\:,\:then\:(p\:,\:r)\varepsilon\:R}$時，R被稱為傳遞的。

等價的

如果R是自反的、對稱的和傳遞的，則R被稱為等價的。

函式

從集合A到B的函式是將B的一個元素分配給A的每個元素。換句話說，如果A的每個元素在集合B中只有一個像，則集合A到B的關係R被稱為函式。

函式的型別

在數學中，研究了各種函式，如下所示。

• 一對一和多對一

• 滿射和入射

• 雙射

讓我們詳細討論每種型別的函式。

一對一和多對一

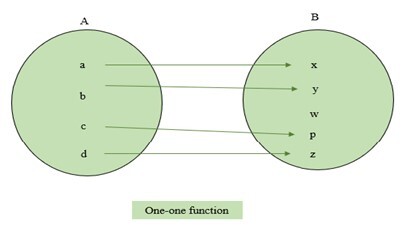
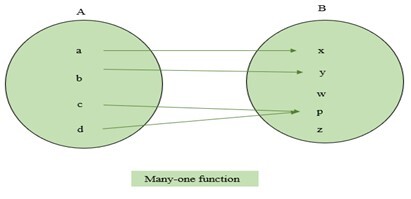
如果集合A的每個元素到集合B的元素的對映都是不同的，則函式$\mathrm{f\:\colon\:A\:\rightarrow\:B}$被稱為一對一函式。它也稱為單射函式。如果集合A的任何元素都與B的多個元素對映，則它被稱為多對一函式。下面顯示了一對一和多對一函式的示例。

滿射和入射

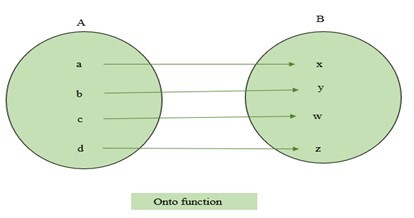
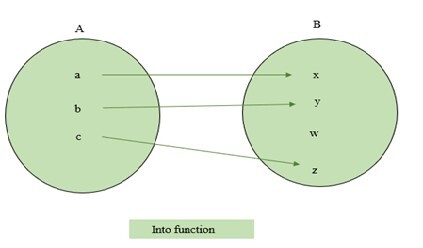
如果B的每個元素都是A在𝑓下某個元素的像，則函式$\mathrm{f\:\colon\:A\:\rightarrow\:B}$被稱為滿射函式。換句話說，如果函式的值域變為B，則它被稱為滿射函式。入射函式是滿射的反義詞。這意味著，如果B的一個元素不是A的某個元素的像，則它被稱為入射函式。下面顯示了一對一和多對一函式的示例。

雙射

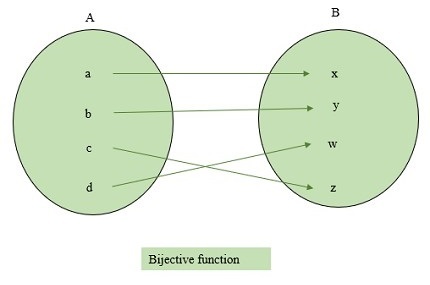
如果一個函式既是一對一函式又是滿射函式，則它被稱為雙射函式。

函式的複合

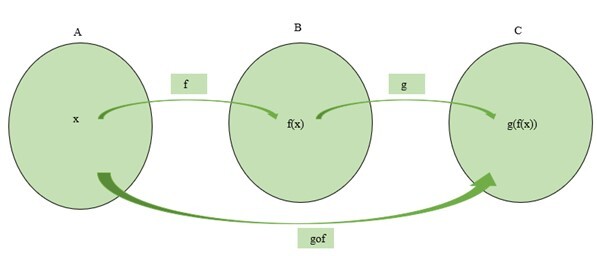
在數學中，兩個函式（例如f和g）產生一個新的函式j（例如），使得

$\mathrm{f(x)\:=\:g(f(x))}$。

讓我們考慮函式$\mathrm{f\:\colon\:A\:\rightarrow\:B}$和$\mathrm{g\:\colon\:B\:\rightarrow\:C}$是兩個函式。上述函式的複合可以寫成$\mathrm{gof\:\colon\:A\:\rightarrow\:C\:and\:gof\:=\:g(f(x))}$ 函式複合的示意圖如下所示。

函式的反函式

如果$\mathrm{gof\:=\:I_{C}\:and\:fog\:=\:I_{B}}$，則函式$\mathrm{g\:\colon\:B\:\rightarrow\:C}$被稱為函式$\mathrm{f\:\colon\:C\:\rightarrow\:B}$的反函式。如果一個函式存在反函式，則它被稱為可逆函式。需要注意的是，可逆函式是雙射函式。

已解決的示例

示例1

讓我們考慮一個集合$\mathrm{P\:=\:\lbrace\:-7\:,\:5\:,\:-6\:,\:3\:\rbrace\:}$，並且關係由$\mathrm{R\:=\:\lbrace\:(-7\:,\:5)\:,\:(-7\:,\:7)\:,\:(5\:,\:5)\:,\:(-6\:,\:3)\:,\:(3\:,\:3)\:,\:(-6\:,\:-6)\:,\:\rbrace\:}$給出。檢查關係是否是等價關係。

解決方案 -

自反性 - 由於$\mathrm{(-7\:,\:-7)\:,\:(5\:,\:5)\:,\:(-6\:,\:-6)\:,\:(3\:,\:3)\:R}$，關係R是自反的。

對稱性 - 關係R不是對稱的，因為$\mathrm{(p\:,\:q)\:R\:,\:but\:(q\:,\:p)}$ 例如$\mathrm{(-7\:,\:5)R\:,\:but\:(5\:,\:7)R}$

傳遞性 - 關係R是傳遞的，因為$\mathrm{(p\:,\:q)R\:,\:but\:(p\:,\:r)\:R}$

∴ 上述關係是自反的和傳遞的。但是，它不滿足對稱性。因此，上述關係不是等價關係。

示例2

如果$\mathrm{f(x)\:=\:3x\:and\:g(x)\:=\:5x\:-\:8}$，則評估fog。

解決方案 -

給出：

$\mathrm{f(x)\:=\:3x\:and\:g(x)\:=\:5x\:-\:8}$

$\mathrm{fog\:=\:f(g(x))\:=\:f(5x\:-\:8)}$

現在將$\mathrm{x\:=\:5x\:-\:8\:}$的值代入$\mathrm{f(x)}$，我們得到

$\mathrm{\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:fog\:=\:3(5x\:-\:8)\:=\:15x\:-\:24}$

結論

本文簡要介紹了關係和函式。本文描述了它們的定義和各種型別。此外，還提供了一些已解決的示例，以更好地理解這一概念。總之，本文可能有助於理解關係和函式的基本概念。

常見問題

1. 所有的關係都是函式。這個說法正確嗎？

不。所有函式都是關係。但是，反過來可能不成立。

2. 恆等函式是什麼意思？

如果集合B的每個元素都給出相同的元素本身作為其像，則該函式被稱為恆等函式。

3. 關係和函式之間有什麼基本區別？

關係對於一個輸入可能有多個輸出。但是，函式對於一個輸入只有一個輸出。所有函式都可以稱為關係。但是，反過來可能不成立。

4. 給出一些關係的現實生活中的例子？

關係的現實生活中的例子是：

• 一種能量飲料中的卡路里數量。

• 油箱中有6.0升柴油行駛的距離。

5. 關係中的定義域是什麼意思？

包含關係所有第一個元素的集合稱為定義域。