整數練習題

---

簡介

• 整數是數學中最重要概念之一，其中大多數與本主題相關。您可以透過練習多個整數練習題來練習此概念。

• 在數學中，整數被描述為可能為正、負或零的數字。

• 但是，這些數字不能構成分數。

• 根據整數練習題，這些數字可以用於執行各種數學運算，包括加法、減法、乘法和除法。

• 根據整數練習題，整數的例子包括 1、2、5、8、-8、-12 和 6。在本教程中，我們將討論整數。

整數

• 拉丁語“integer”表示“整體”或“完整”。因此，整數不包括分數和小數。

• 整數可以包含正數和負數，包括零，是一個沒有小數或分數部分的數字。

• 整數包括 -5、0、1、5、8、97 和 303 等。

• Z 是所有整數的集合，包含以下內容：

正數 - 如果一個數大於零，則它被認為是正數

例如 - 1、2、3 等。

負數 是小於零的數

例如 - -1、-2、-3 等

注意 - 零被描述為既不是正數也不是負數

整數規則

對於整數，指定以下規則：

• 兩個整數的和將是一個整數

• 兩個整數的積將是一個整數

整數代數

整數可用於以下四種基本算術運算：

• 整數的加法

• 整數的減法

• 整數的乘法

• 整數的除法

整數的加法

整數加法規則：

加兩個整數時，使用以下指南：

當兩個整數符號相同時：將它們的絕對值相加，並將結果賦予與輸入整數相同的符號。

當兩個整數符號不同時：確定兩個數的絕對值之間的差，然後將兩個數中較大數的符號加到結果中。

例如，簡化以下方程式 $\mathrm{1\:+\:9\:+\:11}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:給定方程式為\:1\:+\:9\:+\:11}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:21}$

整數的減法

整數減法規則：

要執行兩個整數的減法，請應用以下規則

要執行兩個整數的減法，請應用以下規則：

將減數的符號更改為將運算轉換為加法問題。應用相同的規則來加整數並解決上述步驟中獲得的問題。

例如，簡化以下方程式 $\mathrm{22\:-\:10\:-\:2}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:給定方程式為\:22\:-\:10\:-\:2}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:22\:-\:12}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10}$

整數的乘法和除法

整數乘法或除法規則：

乘或除各個整數的絕對值，結果的符號由一個簡單的規則確定：如果兩個整數符號相同，則結果為正，否則為負。

例如，簡化以下方程式 $\mathrm{100\:\div\:(5\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:給定方程式為\:100\:\div\:(5\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:100\:\div\:20}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:5}$

數軸上的整數

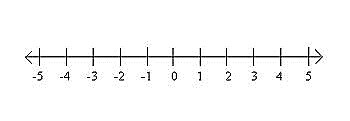
數字的直線以視覺方式顯示為數軸。此線用於比較在無限線上等距間隔的整數，該無限線在兩側水平延伸。

在數軸上，可以視覺化表示正整數和負整數。數軸上整數的表示對於執行數學運算很有用。在數軸上排列整數時，請牢記以下基本注意事項：

• 正整數位於數字零的右側，因為它們大於 0

• 負數位於零的左側，因為它們小於 0。

• 零通常位於中間，因為它既不能是正數也不能是負數。

解題示例

示例 1 - 簡化以下方程式 $\mathrm{2\:+\:8\:-\:(-5)}$

解 - 給定方程式為 $\mathrm{2\:+\:8\:-\:(-5)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10\:-\:(-5)}$.

我們知道兩個負號的乘積得到一個正號，現在應用此規則

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10\:+\:5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:15}$

示例 2 - 簡化以下方程式 $\mathrm{2\:\times\:(-3)\:+\:8\:(-5)}$

解 - 給定方程式為 $\mathrm{2\:\times\:(-3)\:+\:8\:(-5)}$

我們知道正負號的乘積得到一個負號，現在應用此規則

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:2\:\times\:(-3)\:+\:8\:(-5)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:-6\:+\:8\:+\:-5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:-3}$

示例 3 - 簡化以下方程式 $\mathrm{(2\:\times\:4\:+\:8)\:\div\:4}$

解 - 給定方程式為 $\mathrm{(2\:\times\:4\:+\:8)\:\div\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:(8\:+\:8)\:\div\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:16\:\div\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:4}$

示例 4 - 解 $\mathrm{5\:+\:9(2\:\times\:2)\:-\:4}$

解 - 給定方程式為 $\mathrm{5\:+\:9(2\:\times\:2)\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:5\:+\:9(4)\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:5\:+\:36\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:41\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:37}$

示例 5 - 解 $\mathrm{(12\:+\:14)\:\times\:16}$

解 - 給定方程式為 $\mathrm{(12\:+\:14)\:\times\:16}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:26\:\times\:16}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:416}$

示例 6 - 解 $\mathrm{(100\:\div\:20)\:+\:5}$

解 $\mathrm{=\:(100\:\div\:20)\:+\:5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:5\:+\:5}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:10}$

示例 7 - 簡化以下方程式 $\mathrm{900\:\div\:[(25\:\times\:4)\:-\:8\:-\:2]}$

解 - 給定方程式為 $\mathrm{900\:\div\:[(25\:\times\:4)\:-8\:-\:2]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:900\:\div\:[(100)\:-\:8\:-\:2]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:900\:\div\:[(100)\:-\:10]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:900\:\div\:90}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:10}$

示例 8 - 簡化以下方程式 $\mathrm{(25\:\times\:4)\:-\:(20\:\times\:4)}$

解 - 給定方程式為 $\mathrm{(25\:\times\:4)\:-\:(20\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:100\:-\:8}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:20}$

示例 9 - 如果一個單元測試包含 100 道題，每答對一題得 10 分，每答錯一題扣 4 分。如果維諾德正確回答了 75 道題，並且他嘗試了所有問題。維諾德的總分是多少？

解 - 單元測試中的問題總數 = 100

每道正確問題的得分 = 10

每道錯誤問題扣除的分數 = 4

他嘗試的問題總數 = 100

維諾德的總分 $\mathrm{=\:75\:\times\:10\:-\:(25\:\times\:4)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:750\:-\:100}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:650}$

示例 10 - 如果一輛公共汽車以 $\mathrm{10\:\frac{m}{s}}$ 的速度行駛 10 分鐘，則求公共汽車行駛的總距離。

解 $\mathrm{10\:\frac{m}{s}}$

$\mathrm{總時間\:=\:10\:分鐘}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:10\:\times\:60\:=\:600\:秒}$

$\mathrm{公共汽車行駛的距離\:=\:600\:\times\:10}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:600\:米}$

結論

整數練習題涵蓋了整數的加法和減法、多個整數的加法和減法以及不同整數的乘法和除法。整數可以包含正整數和負整數，包括零，是一個沒有小數或分數部分的數字。

常見問題解答

1. 整數是什麼意思？

整數可以包含正整數和負整數，包括零，是一個沒有小數或分數部分的數字

2. 負整數可能嗎？

是的，負整數是可能的。負整數，例如 -1、-2、-3、-4 等，是自然數的加法逆元。

3. 數學中有多少種整數？

整數有三種類型：正整數、零和負整數

4. 正整數是什麼意思？

如果一個數大於零，則它被認為是正數。例如，1、2、3 等。

5. 負整數是什麼意思？

負數是小於零的數。例如 - -1、-2、-3 等

6. 如何在數軸上畫整數？

在數軸上繪製整數需要遵循以下步驟。

• 正整數位於數字零的右側，因為它們大於 0。

• 負數位於零的左側，因為它們小於 0。

• 零通常位於中間，因為它既不能是正數也不能是負數。