平行軸定理

---

引言

物體的轉動慣量 (MOI) 由平行軸定理確定，該定理平行於物體軸線的質量，並且也穿過重力中心。PAT 表明，物體的轉動慣量之和與物體的質量與軸距離平方的乘積定義了 PAT。它有助於找到諸如杆、圓盤等物體的 MOI。在本教程中，將進一步討論平行軸定理。

平行軸定理的歷史

克里斯蒂安·惠更斯在研究復擺時提出了平行軸定理。平行軸定理也稱為惠更斯-施泰納定理，因為它以“克里斯蒂安·惠更斯”和“雅各布·施泰納”命名

平行軸定理

物體的平行軸定理用於評估具有平行於重心軸線的軸線的固體和平面體的 MOI。根據 Abdulghany (2017) 的說法，物體的轉動慣量決定了其在特定平面上的存在狀態。

平行軸定理由物體的慣性繞穿過質量中點的軸的和以及物體的質量乘以兩軸之間距離的平方之積確定（圖書館，2022）。正如王和裡卡多 (2019) 所述，這方面決定了定理的核心。

此定理適用於任何固體，無論其形狀如何。

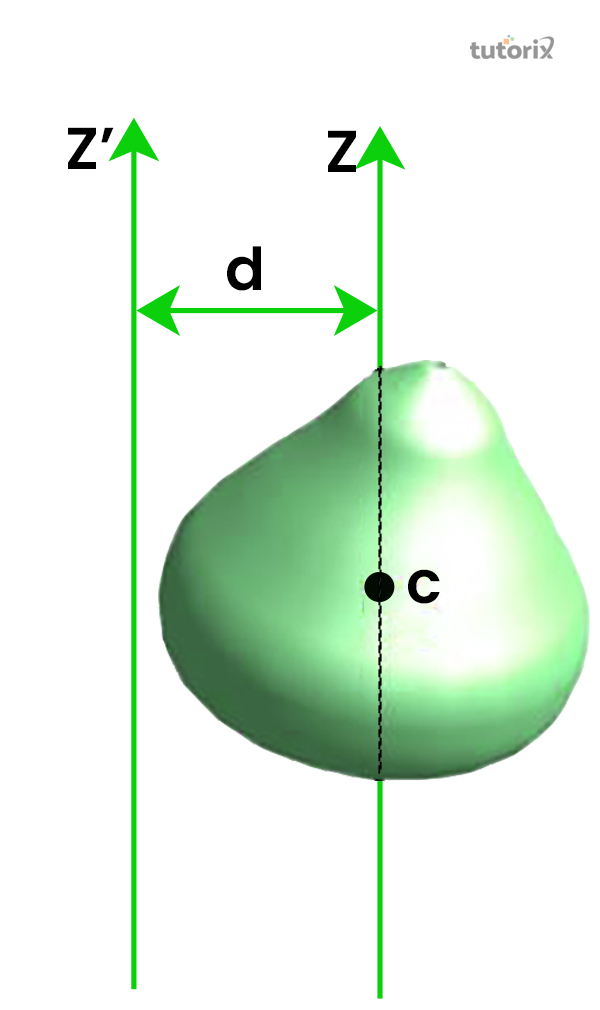
圖 1：平行軸定理

平行軸定理的公式

平行軸定理與固體有關，並透過將物體的轉動慣量與物體的質量乘以兩軸之間距離的平方的乘積相加來確定（phy-astr，2022）。

I = I_x + Ma²

這裡，

這裡，“I”= 物體中的力矩，I_x = 特定剛體的轉動慣量，M = 固體物體的質量，a² 確定兩個特定軸之間的距離的平方。

圖 2：平行軸定理

平行軸定理的推導

此定理將能夠以以下方式推匯出來，假設 I_x 與特定固體物體的轉動慣量相關，並且它正在穿過質量中心（假設軸為 AB），而 I 將是存在於由 A'B' 確定的軸周圍的物體的轉動慣量，並且它存在於距離“a”（phy-astr，2022）處。

現在，當考慮質量為“m”的粒子與重力中心的點之間的距離為“r”時，則可以推匯出 A'B' = r + a

現在

I = Σm ( r + a ) ²

I = ∑m (r² + a² + 2ra)

I = ∑m r² + ∑m a² + ∑2ra

I = I_x  +  a²  ∑m  +  2a∑m r

I = I_x  +  Ma² + 0

I = I_x  +  Ma²

杆的平行軸定理

杆的平行軸定理主要由杆的轉動慣量確定。杆的轉動慣量由以下公式給出：

I = ⅓ ML²

杆的末端與杆中心的距離計算如下：

a = L/2

因此，平行軸定理以以下方式推匯出來

I_x = ⅓ ML² - M(L/2)²

I_x = ⅓ ML² - 1/4 ML²

I_x = 1/12 ML²

轉動慣量

之前已經研究過，慣性與物體為了抵抗特定線性運動狀態而表現出的質量有關，無論是物體處於運動狀態還是靜止狀態（Rempe 等人，2019）。物體的轉動慣量用符號 Im 表示，它僅僅是物體存在的方式以及與其相關的抵抗線性運動狀態或旋轉運動變化的能力的度量。

線上性運動和旋轉運動這兩種情況下，轉動慣量都扮演著完全相同的角色，因此這兩種情況是可以比較的。因此，可以確定物體的轉動慣量是其抵抗其運動狀態變化的能力。

即 Im = Mr²，其中 r 確定粒子與其旋轉軸的垂直距離，M 與旋轉運動中物體的質量有關。但是，轉動慣量與某些因素有關，轉動慣量是標量而不是向量，它對於物體來說不是恆定的，因為它取決於旋轉軸，物體的轉動慣量取決於物體的質量（phy-astgr，2022）。物體的質量越大，轉動慣量越大。隨後，更大的轉動慣量導致質量與其軸之間的更大分離。

圖 3：轉動慣量

垂直軸定理和平行軸定理的應用

垂直軸定理和平行軸定理結合使用以找到任何剛體繞給定軸的轉動慣量。為了計算旋轉運動中任何物體的轉動慣量，使用平行軸定理和垂直軸定理。當知道任何物體繞特定軸的轉動慣量並將其用於計算繞平行於任何其他給定軸的軸的轉動慣量時，使用平行軸定理。如果知道物體在兩個垂直給定軸上的轉動慣量，則使用垂直軸定理計算物體繞第三個垂直軸的轉動慣量。

結論

平行軸定理用於確定物體繞其平行軸的轉動慣量。克里斯蒂安·惠更斯在研究復擺原理時引入了該定理。該定理通常稱為惠更斯-施泰納定理或簡稱為施泰納定理。特定物體在軸平面上的轉動慣量等於物體轉動慣量與質量乘以所涉及的兩軸之間距離的平方之積的和。

常見問題

Q1.什麼是轉動慣量？

任何物體的旋轉慣性稱為轉動慣量。轉動慣量是與物體抵抗運動狀態的趨勢相關的度量；它可以是線性運動或旋轉運動。轉動慣量依賴於物體的質量。物體質量越大，保持慣性狀態的能力就越強。

Q2.何時使用平行軸定理？

當獲得特定物體繞一個軸的轉動慣量時，使用此定理。但是，需要找到另一個平行於第一個軸的軸的轉動慣量。

Q3.平行軸定理的一般表示式是什麼？

平行軸定理通常由表示式 I = I_x + Ma² 確定

這裡 I_x 表示物體繞透過質量中心的軸旋轉的轉動慣量。“M”表示物體的總質量，a 表示透過所考慮的特定物體的質量中心的軸之間的距離。I 表示與旋轉軸平行的物體的轉動慣量。

Q4.誰發現了平行軸定理？

平行軸定理由查爾斯·惠更斯和雅各布·施泰納發現。因此，它也稱為惠更斯-施泰納定理，或者簡單地稱為施泰納定理。

參考文獻

期刊

Abdulghany, A. R. (2017)。轉動慣量的平行軸定理的推廣。美國物理學雜誌，85(10)，791-795。檢索自：https://aapt.scitation.org/doi/full/10.1119/1.4994835

Rempe, D.、Sridhar, S.、Wang, H. 和 Guibas, L. (2019)。學習 3D 剛體的通用最終狀態動力學。在 IEEE/CVF 計算機視覺和模式識別研討會論文集中（第 17-20 頁）。檢索自：http://openaccess.thecvf.com

Wang, J. 和 Ricardo, B. (2019)。轉動慣量計算的壓縮方法。物理教師，57(8)，551-554。檢索自：https://www.researchgate.net/profile/Bernard-Ricardo/publication/336707332_Squashing_Method_for_Moment_of_Inertia_Calculations/links/5dc3761a299bf1a47b1c03fa/Squashing-Method-for-Moment-of-Inertia-Calculations.pdf

網站

圖書館，2022年。關於慣性簡介：平行軸定理。檢索自：https://pressbooks.library.upei.ca/statics/chapter/inertia-intro-parallel-axis-theorem/ [檢索日期：2022年6月7日]

phy-astgr，2022年。關於轉動慣量。檢索自：http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html [檢索日期：2022年6月7日]

phy-astr，2022年。關於平行軸定理。檢索自：http://hyperphysics.phy-astr.gsu.edu/hbase/parax.html [檢索日期：2022年6月7日]