證明兩條直線分別垂直於兩條平行線，則這兩條直線互相平行。

 已知：

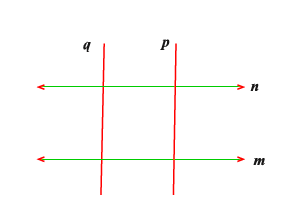
兩條直線 m 和 n 平行，另兩條直線 p 和 q 分別垂直於 m 和 n。

或者 𝑝⊥𝑚 且 𝑝⊥𝑛，𝑞⊥𝑚 且 𝑞⊥𝑛

證明： 𝑝∥𝑞

證明：

由於，𝑚∥𝑛 且 p 垂直於 m 和 n。

所以，

p 垂直於 m …(i)

p 垂直於 n …(ii)

由於，𝑚∥𝑛 且 q 垂直於 m 和 n。

所以，

q 垂直於 m …(iii)

q 垂直於 n …(iv)

 由式 (i) 和 (iii) [或由 (ii) 和 (iv)]，得到 𝑝 ∥𝑞。[如果兩條直線都垂直於同一條直線，則這兩條直線互相平行] 因此，𝑝 ∥𝑞。

教程點

更新時間： 2022年10月10日

112 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習