資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究從邊長為 10 釐米的正方形紙片四個角上分別剪去相同大小的正方形，如何確定剪去的正方形的邊長，才能使折成的無蓋長方體的體積最大？
已知
正方形紙片的邊長 $= 10 cm$。
從正方形紙片的四個角上剪去四個相同的正方形。
求解
我們需要找到剪去的正方形的邊長，使得由紙片折成的長方體的體積最大。
解：
設剪去的正方形的邊長為 'x' cm。
剪去正方形後，剩餘正方形紙片的邊長 $=10 - x - x = 10 - 2x $。
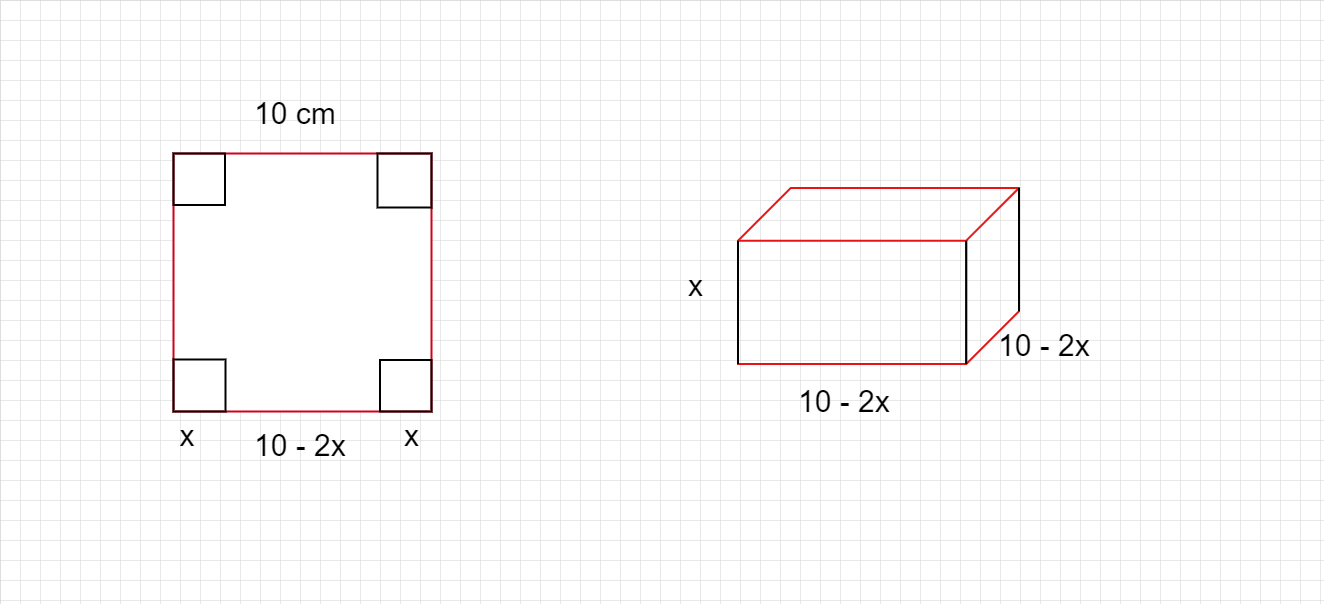
根據圖形，
長方體的長 $= 10 - 2x $
長方體的寬 $= 10 - 2x $
長方體的高 $= x $
我們需要找到 'x' 的值，使得長方體的體積最大。
長方體的體積 $= 長 \times 寬 \times 高 $
長方體的體積 $= (10 - 2x) \times (10 - 2x) \times x $
要從給定的紙片上折成長方體，我們可以剪去邊長為
1 cm、2 cm、3 cm、4 cm 的正方形。
當 $x = 1$ 時
長方體的體積 $= (10 - 2(1)) \times (10 - 2(1)) \times 1 $
$ = (10 - 2) \times (10 - 2) \times 1 $
$= 8 \times 8 \times 1 $
長方體的體積 $= 64 cm^3$。
當 $x = 2$ 時
長方體的體積 $= (10 - 2(2)) \times (10 - 2(2)) \times 2 $
$ = (10 - 4) \times (10 - 4) \times 2 $
$= 6 \times 6 \times 2 $
長方體的體積 $= 72 cm^3$。
當 $x = 3$ 時
長方體的體積 $= (10 - 2(3)) \times (10 - 2(30)) \times 3 $
$ = (10 - 6) \times (10 - 6) \times 3 $
$= 4 \times 4 \times 3 $
長方體的體積 $= 48 cm^3$。
當 $x = 4$ 時
長方體的體積 $= (10 - 2(4)) \times (10 - 2(4)) \times 4 $
$ = (10 - 8) \times (10 - 8) \times 4 $
$= 2 \times 2 \times 4 $
長方體的體積 $= 16 cm^3$。
因此，當 $x = 2$ 時，長方體的體積 $= 72 cm^3$。這是最大體積。
所以，**為了獲得長方體的最大體積，剪去的正方形的邊長應為 2 cm。**
85 次檢視
