利用勾股定理，根據下圖所示的b和c，確定AD的長度。

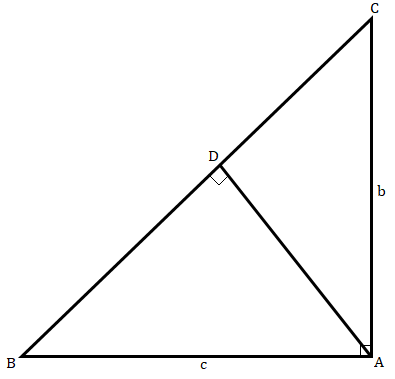
已知

在△ABC中，∠A = 90°。

在△ABD中，∠ADB = 90°。

在△ACD中，∠ADC = 90°。

 要求

我們必須用b和c表示AD的長度。

解答

在△ABC中，

根據勾股定理，

BC² = AB² + AC²

BC² = c² + b²

BC = √(c² + b²)

在△ABD和△ABC中，

∠B = ∠B (公共角)

∠ADB = ∠BAC = 90°

因此，

△ABD ~ △CBA (根據AA相似)

這意味著，

AB/CB = AD/CA (相似三角形的對應邊成比例)

c/√(c² + b²) = AD/b

AD = bc/√(c² + b²)

用b和c表示AD的長度為 bc/√(b² + c²) 。

Tutorialspoint

更新於：2022年10月10日

瀏覽量：127

開啟你的職業生涯

完成課程獲得認證

開始學習