證明圓周角大於半圓的角小於直角。

待辦事項

我們必須證明圓周角大於半圓的角小於直角。

解答

設在以O為圓心的圓中，大於半圓的弓形ACB內接有∠ACB。

連線OA和OB。

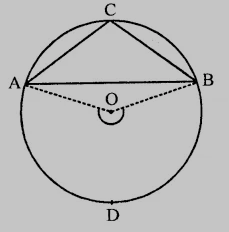
弧ADB在圓心處構成∠AOB，在圓周其餘部分構成∠ACB。

因此，

∠ACB = ½∠AOB

∠AOB < 180°

這意味著，

∠ACB < 90°

∠ACB < 90°

因此∠ACB < 90°

教程點

更新於：2022年10月10日

67 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習