點\( (-2,4),(3,-1),(-1,0) \), \( (1,2) \) 和 \( (-3,-5) \) 分別位於哪個象限或哪條座標軸上？透過在笛卡爾平面中定位這些點來驗證你的答案。

待辦事項

我們需要找到點\( (-2,4),(3,-1),(-1,0) \), \( (1,2) \) 和 \( (-3,-5) \) 位於哪個象限或哪條座標軸上。

解答： 

為了找到點$(-2, 4), (3, -1), (-1, 0), (1, 2)$ 和 $(-3, -5)$ 所在的象限或座標軸，我們將這些點繪製在圖上，如下所示。

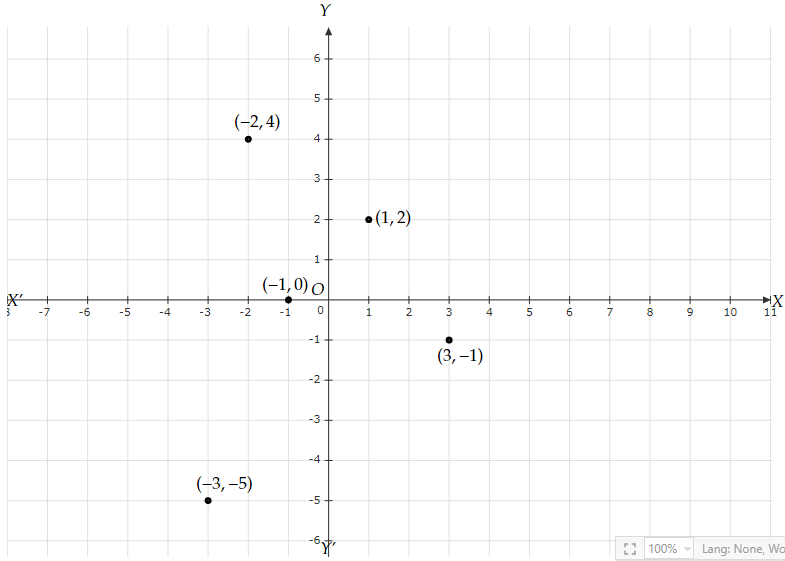
從上圖中，我們可以得出以下結論：

點 $(-2, 4)$ 位於第 $2$ 象限。

點 $(3, -1)$ 位於第 $4$ 象限。

點 $(-1, 0)$ 位於負 X 軸上。

點 $(1, 2)$ 位於第 $1$ 象限。

點 $(-3, -5)$ 位於第 $3$ 象限。

教程點

更新於： 2022年10月10日

1K+ 瀏覽量

開啟你的 職業生涯

透過完成課程獲得認證

開始學習