在△ABC中，線段PQ與AB相交於點P，與AC相交於點Q，且PQ∥BC，PQ將△ABC分成面積相等的兩個部分。求BP/AB的值。

已知

在△ABC中，線段PQ與AB相交於點P，與AC相交於點Q，且PQ∥BC，PQ將△ABC分成面積相等的兩個部分。

求解

我們需要求BP/AB的值。

解題步驟

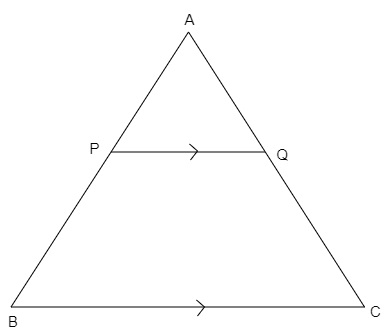
PQ∥BC，且ar(△APQ)=ar(梯形BCQP)=1/2ar(△ABC)

在△APQ和△ABC中，

∠PAQ=∠BAC (公共角)

∠APQ=∠ABQ (同位角)

因此，

△APQ～△ABC (AA相似)

這意味著，

ar(△APQ)/ar(△ABC)=(AP/AB)² (相似三角形面積定理)

1/2ar(△ABC)/ar(△ABC)=(AP/AB)²

(AP/AB)²=1/2

AP/AB=1/√2

AP=AB/√2

BP=AB-AP

BP=AB-AB/√2

BP=AB(√2-1)/√2

因此，

BP/AB=AB(√2-1)/√2 / AB

= (√2-1)/√2

=(√2-1)/√2

BP/AB的值為(√2-1)/√2。

教程點

更新於：2022年10月10日

瀏覽量：108

開啟你的職業生涯

完成課程獲得認證

開始學習