在給定圖形中，$RT \parallel SQ$。如果$\angle QPS = 110^{\circ}$，$\angle PQS = 40^{\circ}$，$\angle PSR = 75^{\circ}$，$\angle QRS = 65^{\circ}$，則求$\angle QRT$的值。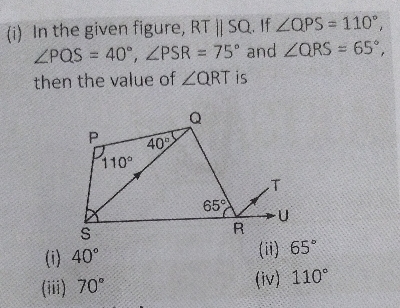

已知：在給定圖形中，$RT \parallel SQ$。如果$\angle QPS = 110^{\circ}$，$\angle PQS = 40^{\circ}$，$\angle PSR = 75^{\circ}$，$\angle QRS = 65^{\circ}$。

求解：求$\angle QRT$的值

解

從圖中

在$\vartriangle PQS$中，

$\angle PQS + \angle QPS + \angle PSQ = 180^o$

$\Rightarrow \angle PSQ = 180^o - \angle QPS - \angle PQS = 180^o - 110^o - 40^o = 30^o$ **(原文有誤，應該是30度)**

已知 $\angle PSR = 75^o$

$\Rightarrow \angle PSQ + \angle QSR = 75^o$

$\Rightarrow \angle QSR = 75^o - \angle PSQ = 75^o - 30^o = 45^o$

在$\vartriangle QSR$中

$\angle QRS + \angle QSR + \angle SQR = 180^o$

$\angle SQR = 180^o - \angle QRS - \angle QSR = 180^o - 65^o - 45^o = 70^o$ **(原文計算有誤)**

因為 $RT \parallel SQ$

$\angle QRT = \angle SQR = 70^o$       [內錯角]

教程點

更新於：2022年10月10日

363 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習