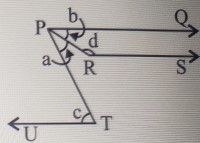
在給定的圖形中，PQ、RS 和 UT 是平行線。如果 c=75° 且 a=(2/5)c。


A. 92°
B. 115°
C. 112.5°
D. 135.5°

已知

在給定的圖形中，PQ、RS 和 UT 是平行線。如果 c=75° 且 a=(2/5)c。
求解：

我們需要求 $b+\frac{d}{2}$ 的值。
解

$PQ\parallel\ RS\parallel\ UT$

$c=75^o$

$a=\frac{2}{5}c=\frac{2}{5}\times75^o=2\times15^o=30^o$

$PQ\parallel\ UT$，PT 為橫截線。

因此，

$c=a+b$ (內錯角)

$75^o=30^o+b$

$b=75^o-30^o$

$b=45^o$

$PQ\parallel\ RS$，PR 為橫截線。

因此，

$b+d=180^o$ (同旁內角互補)

$45^o+d=180^o$

$d=180^o-45^o$

$d=135^o$

這意味著，

$b+\frac{d}{2}=45^o+\frac{135^o}{2}=45^o+67.5^o$

$=112.5^o$

選項 C 是正確答案。

教程點

更新於：2022年10月10日

34 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習