資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如圖所示，射線$OS$垂直於直線$POQ$。射線$OR$和射線$OT$分別是$\angle POS$和$\angle SOQ$的角平分線。如果$\angle POS = x$，求$\angle ROT$。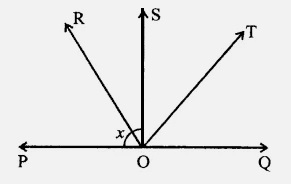
"\n
已知
射線$OS$垂直於直線$POQ$。
射線$OR$和射線$OT$分別是$\angle POS$和$\angle SOQ$的角平分線。
$\angle POS = x$。
求解
我們需要求$\angle ROT$。
解答
$\angle POS = x$
因此，
$\angle POS + \angle QOS = 180^o$ (線性對)
$x + \angle QOS = 180^o$
$\angle QOS = 180^o - x$
$OR$和$OT$分別是$\angle POS$和$\angle QOS$的角平分線。
這意味著，
$\angle \mathrm{ROS}=\frac{x}{2}$
$\angle \mathrm{TOS}=\frac{180^{\circ}-x}{2}$
$\angle \mathrm{ROT}=\angle \mathrm{ROS}+\angle \mathrm{TOS}$
$\angle \mathrm{ROT}=\frac{x}{2}+\frac{180^{\circ}-x}{2}$
$\angle \mathrm{ROT}=\frac{x+180^{\circ}-x}{2}$
$\angle \mathrm{ROT}=\frac{180^{\circ}}{2}$
$\angle \mathrm{ROT}=90^{\circ}$
因此，$\angle \mathrm{ROT}=90^{\circ}$。
更新於: 2022年10月10日
246 次瀏覽
廣告