如圖所示，∠AOF 和∠FOG 構成一對鄰補角。∠EOB = ∠FOC = 90°，且∠DOC = ∠FOG = ∠AOB = 30°。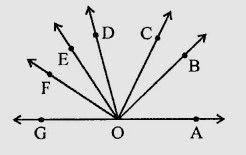求∠FOE 的度數。

已知

∠AOF 和∠FOG 構成一對鄰補角。∠EOB = ∠FOC = 90°，且∠DOC = ∠FOG = ∠AOB = 30°。

要求

我們必須求出∠FOE、∠COB 和∠DOE 的度數。

解答

我們知道：

一條直線上角度之和為 180°。

因此：

∠BOE + ∠AOB + ∠EOG = 180°

30° + 90° + ∠EOG = 180°

∠EOG = 180° - 30° - 90°

∠EOG = 60°

∠FOG = 30°

⇒ ∠FOE = 60° - 30° = 30°

∠COD = 30°，∠COF = 90°

∠DOF = 90° - 30°

∠DOF = 60°

∠DOE = ∠DOF - ∠EOF

∠DOE = 60° - 30° = 30°

∠BOC = ∠BOE - ∠COE

∠BOC = 90° - 30° - 30°

∠BOC = 90° - 60° = 30°

教程點

更新於：2022年10月10日

76 次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習