如何在數軸上表示有理數和無理數？

數軸上的有理數

 

要在數軸上表示一個正有理數，請按照以下步驟操作

為了在數軸上表示分數，我們需要將兩個整數之間的線段分成 'n' 等份，其中 n 表示分數的分母。

因此，

如果我們要在數軸上表示分數 $\frac{1}{5}$，我們需要將 0 和 1 之間的線段分成五等份。

在上圖中，點 A 表示分數 $\frac{1}{5}$。


要表示負有理數，請按照以下步驟操作

例如，


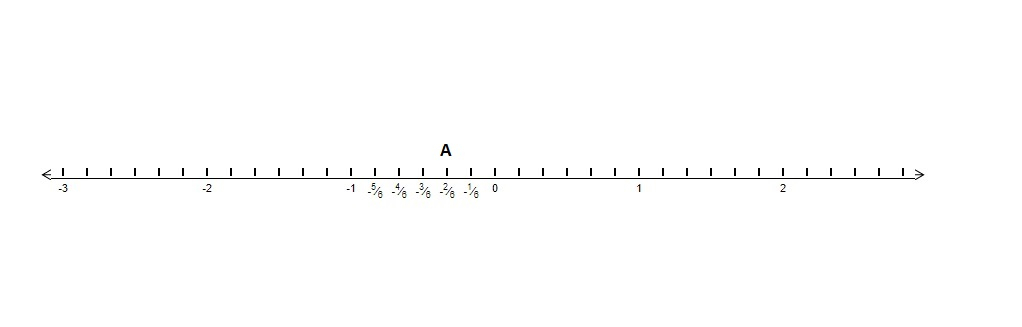
要在數軸上表示 $\frac{-2}{6}$，


1) 畫一條數軸。


2) 由於數 $\frac{-2}{6}$ 是一個負數，因此它將在零的左側。The number$\frac{-2}{6}$ 位於 0 和 $-1$ 之間


3) 將 0 和 $-1$ 之間的線段分成 6 份（這裡 6 是分母）。


4) 向左移動兩部分到 0 （這裡 2 是分子）。


5) 因此，A 是所需點。

數軸上無理數的表示

要表示無理數，我們應該使用勾股定理

Hypotenuse2=Base2+Height2 Hypotenuse^{2}= Base^{2}+ Height^{2}" role="presentation" style="display: inline; line-height: normal; font-size: 16.94px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">Hypotenuse^{2}= Base^{2}+ Height^{2}

  • 現在首先畫一條數軸，並標記 '0'、'1' 和 '2'
  • 以 1 個單位為長度，從 '2' 畫一條線，使其垂直於該線。
  • 現在連線點 (0) 和新線段 1 個單位長度的端點。
  • 構造了一個直角三角形。
  • 現在讓我們將三角形命名為 ABC，使得 BC 為高（垂直），AB 為三角形的底，AC 為直角三角形 ABC 的斜邊。

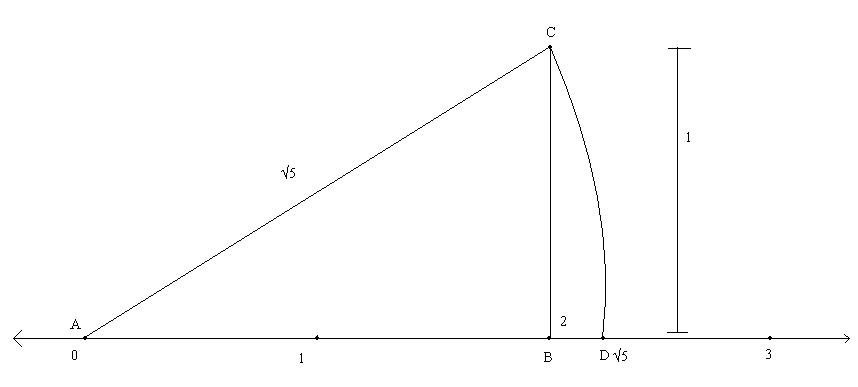
你知道 AC2=22+12 A C^{2}=2^{2}+1^{2}

AC2 = 4 + 1
AC2=5 A C^{2}=5 " role="presentation" style="display: inline-table; line-height: normal; font-size: 16.94px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;"> A C^{2}=5" role="presentation" style="color: rgb(204, 0, 0); font-style: italic; transition: none 0s ease 0s; display: inline; position: relative; border: 0px; padding: 0px; margin: 0px; vertical-align: 0px; line-height: normal;">A C^{2}=5

更新於: 2022年10月10日

90 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

立即開始
廣告

© . All rights reserved.