資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究已知 $x-\sqrt{5}$ 是多項式 $x^{3} -3\sqrt{5} x^{2} -5x+15\sqrt{5}$ 的一個因式，求該多項式的所有零點。
已知： $x-\sqrt{5}$ 是多項式 $x^{3} -3\sqrt{5} x^{2} -5x+15\sqrt{5}$ 的一個因式。
求解：求出該多項式的所有零點。
解：
設 $P(x) =x^{3} -3\sqrt{5} x^{2} -5x+15\sqrt{5}$。
因為 $x-\sqrt{5}$ 是該多項式的一個因式。
現在我們令 $x=\sqrt{5}$
$P(\sqrt{5}) = (\sqrt{5})^{3} -3\sqrt{5}(\sqrt{5})^{2} -5(\sqrt{5}) +15\sqrt{5} = 5\sqrt{5} - 15\sqrt{5} - 5\sqrt{5} + 15\sqrt{5} = 0$
因此 $(x-\sqrt{5})$ 是一個因式
$=0$
$\therefore \ (x-\sqrt{5})$ 是 $P(x)$ 的一個因式
$\therefore \ (x+\sqrt{5})(x-\sqrt{5}) =x^{2} -5$ 是 $P(x)$ 的一個因式
用 $x^{2} -5$ 除以給定的多項式。
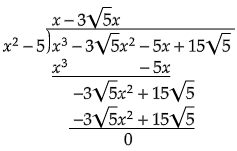
$\therefore \ x-3\sqrt{5}$ 是該多項式的因式。
$\therefore \ x-3\sqrt{5} =0$
$\Rightarrow x=3\sqrt{5}$
$\therefore \sqrt{5} ,\ -\sqrt{5} $ 和 $3\sqrt{5}$ 是該多項式的零點。
更新於： 2022年10月10日
62 次瀏覽
廣告