以下是100名學生的智商分佈。求智商的中位數。

智商	55-64	65-74	75-84	85-94	95-104	105-114	115-124	125-134	135-144
學生人數	1	2	9	22	33	22	8	2	1

已知

100名學生的分佈。

要求

我們需要求智商的中位數。

解答

將組別轉換為互斥形式，然後形成其累積頻率表，如下所示：

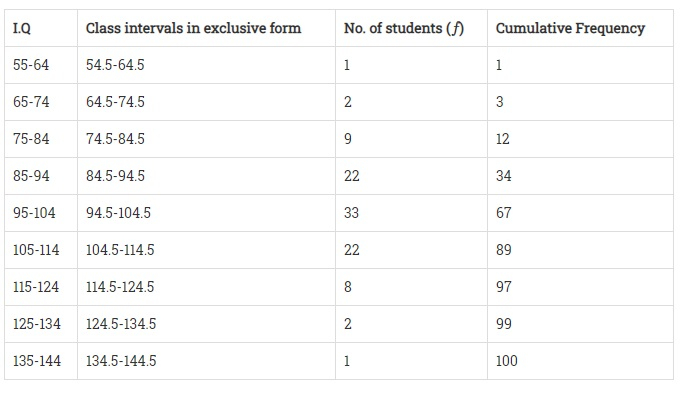
這裡，

$N = 100$

$\frac{N}{2} = \frac{100}{2} = 50$

恰好大於$\frac{N}{2}$的累積頻率是67，對應的組別是94.5 – 104.5。

這意味著，94.5 – 104.5是中位陣列。

因此，

$l = 94.5, f = 33, F = 34$ 且 $h = (104.5 - 94.5) = 10$

中位數 $=\mathrm{l}+\frac{\frac{\mathrm{N}}{2}-\mathrm{F}}{\mathrm{f}} \times \mathrm{h}$

$=94.5+\frac{50-34}{33} \times 10$

$=94.5+\frac{16}{33} \times 10$

$=94.5+\frac{160}{33}$

$= 94.5 + 4.85$

$= 99.35$

智商的中位數是99.35。 

教程點

更新於： 2022年10月10日

61 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習