資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
時尚研究
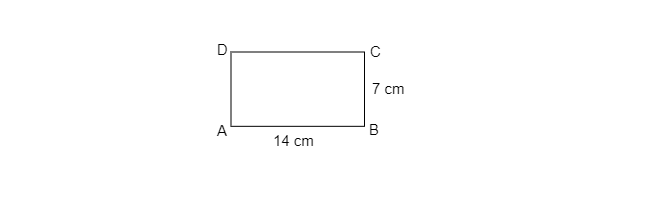
法律研究求由旋轉尺寸為 14 cm × 7 cm 的塑膠薄片（如圖所示）形成的圓柱體的體積。(i) 繞 AB 旋轉；(ii) 繞 BC 旋轉。
已知：一個圓柱體是由旋轉尺寸為 14 cm × 7 cm 的塑膠薄片（如圖所示）形成的。
要求：求當塑膠薄片分別繞：(i) AB 和 (ii) BC 旋轉時，圓柱體的體積。
解答
(i) 當塑膠薄片繞 AB 旋轉時
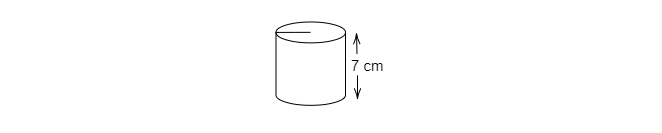
圓柱體的高 (h) = 7 cm
AB 成為圓柱體的周長。設圓柱體的半徑為 r。
⇒ 2πr = 14
⇒ r = 14 / (2π)
⇒ r = 7/π
∴ 圓柱體的體積 V = πr²h
⇒ V = π × (7/π)² × 7
⇒ V = π × (49/π²) × 7
⇒ V = (49 × 7) / π ≈ 109.09 cm³
⇒ V ≈ 109.09 cm³
(ii) 當塑膠薄片繞 BC 旋轉時
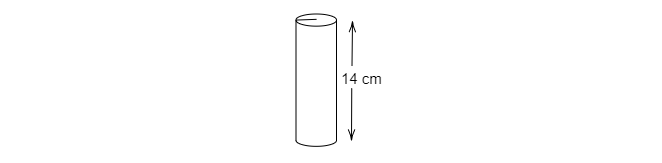
AB 是圓柱體的高。CD 是圓柱體的周長。
⇒ 2πr = 7
⇒ r = 7 / (2π)
新圓柱體的體積 V = πr²h
⇒ V = π × (7/(2π))² × 14
⇒ V = π × (49/(4π²)) × 14
⇒ V = (49 × 14) / (4π) ≈ 54.19 cm³
⇒ V ≈ 54.19 cm³
更新於：2022年10月10日
119 次瀏覽
廣告