一個三角形的三條邊長分別為 5 釐米、12 釐米和 13 釐米。求從與 13 釐米邊相對的頂點到該邊的垂線的長度。
"\n

已知

一個三角形的三條邊長分別為 5 釐米、12 釐米和 13 釐米。

要求

我們要求出從與 13 釐米邊相對的頂點到該邊的垂線的長度。

 解答

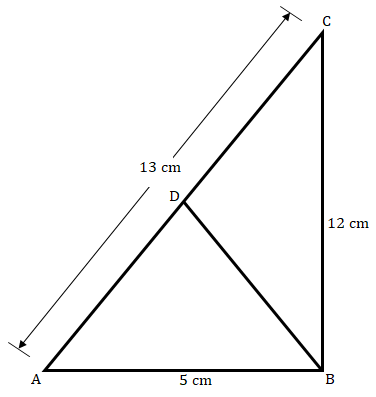
根據圖形，

$AC^2 = (13)^2\ cm^2 = 169\ cm^2$。

$AB^2 = (5)^2\ cm^2 = 25\ cm^2$。

$BC^2 = (12)^2\ cm^2 = 144\ cm^2$。

$AB^2+BC^2=(25+144)\ cm^2=169\ cm^2$

因此，

$AB^2+BC^2=AC^2$

$∆ABC$ 是一個直角三角形，∠B 為直角。

設 $BD$ 為從 $B$ 到 $AC$ 的垂線的長度。

$∆ABC$ 的面積 $= \frac{1}{2}(BC \times BA)$

                         $= \frac{1}{2}(12 \times 5)$

                        $= 30\ cm^2$

$∆ABC$ 的面積 $= \frac{1}{2}(AC \times BD)$

                         $=\frac{1}{2}(13 \times BD)$

                        $=\frac{1}{2}(13 \times BD)$

$30\ cm^2=\frac{1}{2}(13 \times BD)$

$BD=\frac{30\times2}{13}$

$BD=\frac{60}{13}$

$BD=4.6\ cm$

從與 13 釐米邊相對的頂點到該邊的垂線的長度為 $4.6\ cm$。

教程點

更新於: 2022年10月10日

548 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習