一頭小牛用一根長\( 6 \mathrm{~m} \)的繩子系在一個邊長為\( 20 \mathrm{~m} \)的正方形草坪的角上。如果繩子的長度增加\( 5.5 \mathrm{~m} \)，求小牛可以吃草的草坪面積的增加量。

已知：

一頭小牛用一根長\( 6 \mathrm{~m} \)的繩子系在一個邊長為\( 20 \mathrm{~m} \)的正方形草坪的角上。

繩子的長度增加了\( 5.5 \mathrm{~m} \)。

要求：

我們要求出小牛可以吃草的草坪面積的增加量。

解答

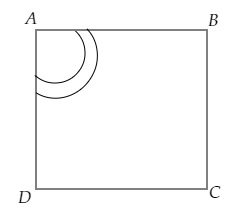
設小牛系在正方形草坪的角A處。
面積的增加量等於兩個中心角均為$90^o$，半徑分別為$(6+ 5.5)\ m=11.5\ m$和$6\ m$的扇形面積的差，即圖中陰影部分。

半徑為$r$，圓心角為$\theta$的扇形面積為$\frac{\theta}{360} \times \pi \times r^{2}$

因此，

面積增加量$=[\frac{90}{360} \times \pi \times 11.5^{2}-\frac{90}{360} \pi \times 6^{2}] \mathrm{m}^{2}$

$=\frac{\pi}{4} \times(11.5+6)(11.5-6) \mathrm{m}^{2}$

$=\frac{22}{7 \times 4} \times 17.5 \times 5.5 \mathrm{~m}^{2}$

$=75.625 \mathrm{~m}^{2}$

小牛可以吃草的草坪面積的增加量為$75.625 \mathrm{~m}^{2}$。

教程點

更新於： 2022年10月10日

75 次瀏覽

開啟你的職業生涯

完成課程獲得認證

立即開始