資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如果△ABC的三條邊的中點分別為D(-1/2, 5/2), E(7, 3) 和 F(7/2, 7/2)，求△ABC的面積。
已知
D(-1/2, 5/2), E(7, 3) 和 F(7/2, 7/2) 是△ABC三條邊的中點。
求解
我們需要求出△ABC的面積。
解題步驟
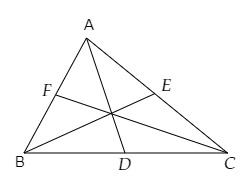
設A(x₁, y₁), B(x₂, y₂) 和 C(x₃, y₃) 是△ABC的頂點。
座標為(x₁, y₁) 和 (x₂, y₂) 的線段的中點座標為((x₁+x₂)/2, (y₁+y₂)/2)
D(-1/2, 5/2)是BC的中點。
(x₂+x₃)/2 = -1/2
=> x₂ + x₃ = -1 ......(i)
(y₂+y₃)/2 = 5/2
=> y₂ + y₃ = 5 ......(a)
類似地，
E(7, 3)是CA的中點。
(x₃+x₁)/2 = 7
=> x₃ + x₁ = 14 ......(ii)
(y₃+y₁)/2 = 3
=> y₃ + y₁ = 6 ......(b)
F(7/2, 7/2)是AB的中點。
(x₁+x₂)/2 = 7/2
=> x₁ + x₂ = 7 ......(iii)
(y₁+y₂)/2 = 7/2
=> y₁ + y₂ = 7 ......(c)
將(i), (ii) 和 (iii) 三式相加，得到：
2(x₁ + x₂ + x₃) = 20
=> x₁ + x₂ + x₃ = 10 ......(iv)
分別從(iv)式中減去(i), (ii) 和 (iii)式，得到：
x₁ = 11, x₂ = -4, x₃ = 3
將(a), (b) 和 (c) 三式相加，得到：
2(y₁ + y₂ + y₃) = 18
=> y₁ + y₂ + y₃ = 9 ......(d)
分別從(d)式中減去(a), (b) 和 (c)式，得到：
y₁ = 4, y₂ = 3, y₃ = 2
因此，△ABC的頂點座標為A(11, 4), B(-4, 3) 和 C(3, 2)
△ABC的面積為：Δ = 1/2[x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)]
Δ = 1/2[11(3-2) + (-4)(2-4) + 3(4-3)]
= 1/2[11×1 + (-4)(-2) + 3(1)]
= 1/2(11 + 8 + 3)
= 22/2
\( =11 \)
△ABC的面積為11平方單位。
瀏覽量：50
