圖論速查指南

圖論 - 緒論

在數學和計算機科學領域，圖論是研究圖的學科，它關注邊和頂點之間的關係。它是一個熱門學科，其應用遍及計算機科學、資訊科技、生物科學、數學和語言學等多個領域。事不宜遲，讓我們從定義圖開始。

什麼是圖？

圖是一組物件的圖形表示，其中一些物件對透過連結連線。相互連線的物件由稱為頂點的點表示，連線頂點的連結稱為邊。

正式地說，圖是一對集合(V, E)，其中V是頂點的集合，E是連線頂點對的邊的集合。請看下面的圖：

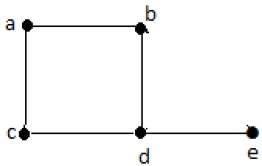
在上圖中：

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

圖論的應用

圖論在各個工程領域都有應用：

電氣工程 - 圖論的概念廣泛應用於電路連線的設計。連線的型別或組織稱為拓撲結構。一些拓撲結構的例子包括星型、橋型、序列和並行拓撲結構。

計算機科學 - 圖論用於演算法的研究。例如：

克魯斯卡爾演算法
普里姆演算法
迪傑斯特拉演算法

計算機網路 - 網路中相互連線的計算機之間的關係遵循圖論的原理。

科學 - 物質的分子結構和化學結構、生物體的DNA結構等都用圖表示。

語言學 - 語言的句法樹和語言的語法使用圖。

一般 - 城市之間的路線可以用圖表示。描繪分層有序資訊（如家譜）可以用一種稱為樹的特殊型別的圖來表示。

圖論 - 基礎知識

圖是點和連線點的線的圖表。它至少有一條線連線一組兩個頂點，沒有頂點連線自身。圖論中的圖的概念建立在一些基本術語之上，例如點、線、頂點、邊、頂點的度、圖的性質等。在本節中，我們將介紹這些圖論的基礎知識。

點

點是一維、二維或三維空間中的特定位置。為了更好地理解，可以用字母表示一個點。可以用點來表示它。

例子

這裡，點是一個名為“a”的點。

線

線是兩點之間的連線。可以用實線表示。

例子

這裡，“a”和“b”是點。這兩點之間的連線稱為線。

頂點

頂點是多條線相交的點。它也稱為節點。與點類似，頂點也用字母表示。

例子

這裡，頂點用字母“a”命名。

邊

邊是連線兩個頂點的線的數學術語。許多邊可以從單個頂點形成。沒有頂點，就不能形成邊。邊必須有一個起始頂點和一個結束頂點。

例子

這裡，“a”和“b”是兩個頂點，它們之間的連線稱為邊。

圖

圖“G”定義為G = (V, E)，其中V是圖中所有頂點的集合，E是圖中所有邊的集合。

示例1

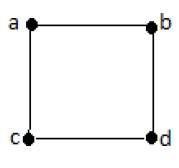
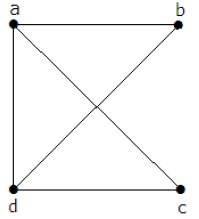
在上例中，ab、ac、cd和bd是圖的邊。類似地，a、b、c和d是圖的頂點。

示例2

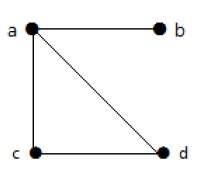
在這個圖中，有四個頂點a、b、c和d，以及四條邊ab、ac、ad和cd。

環

在一個圖中，如果從頂點到自身畫一條邊，則稱為環。

示例1

在上圖中，V是一個頂點，它有一條邊(V, V)形成一個環。

示例2

在這個圖中，在頂點a和頂點b處形成了兩個環。

頂點的度

它是與頂點V相鄰的頂點數。

表示法 - deg(V)。

在一個具有n個頂點的簡單圖中，任何頂點的度為：

deg(v) ≤ n – 1 ∀ v ∈ G

一個頂點可以與除自身之外的所有其他頂點形成邊。因此，頂點的度數最多為圖中頂點數減1。這個1是自頂點，因為它不能自己形成環。如果任何頂點上都有環，則它不是簡單圖。

頂點的度數可以考慮圖的兩種情況：

無向圖
有向圖

無向圖中頂點的度數

無向圖沒有有向邊。請考慮以下示例。

示例1

請看下面的圖：

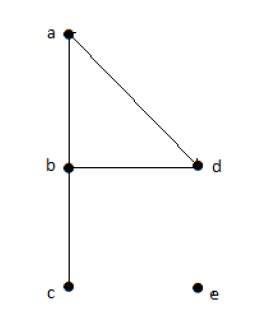
在上圖中：

deg(a) = 2，因為在頂點“a”處有2條邊。
deg(b) = 3，因為在頂點“b”處有3條邊。
deg(c) = 1，因為在頂點“c”處形成1條邊。
所以“c”是懸掛頂點。
deg(d) = 2，因為在頂點“d”處有2條邊。
deg(e) = 0，因為在頂點“e”處沒有形成邊。
所以“e”是孤立頂點。

示例2

請看下面的圖：

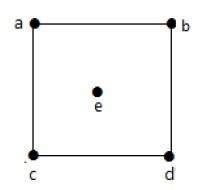
在上圖中：

deg(a) = 2, deg(b) = 2, deg(c) = 2, deg(d) = 2, deg(e) = 0。

頂點“e”是孤立頂點。該圖沒有任何懸掛頂點。

有向圖中頂點的度數

在有向圖中，每個頂點都有一個入度和一個出度。

圖的入度

頂點V的入度是進入頂點V的邊的數量。
表示法 - deg−(V)。

圖的出度

頂點V的出度是從頂點V出去的邊的數量。
表示法 - deg+(V)。

請考慮以下示例。

示例1

請看下面的有向圖。頂點“a”有兩條邊，“ad”和“ab”，它們向外延伸。因此，它的出度為2。同樣，有一條邊“ga”指向頂點“a”。因此，“a”的入度為1。

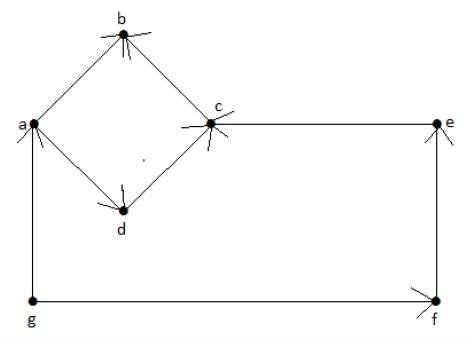
其他頂點的入度和出度如下表所示：

頂點	入度	出度
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

示例2

請看下面的有向圖。頂點“a”有一條邊“ae”從頂點“a”向外延伸。因此，它的出度為1。同樣，該圖有一條邊“ba”指向頂點“a”。因此，“a”的入度為1。

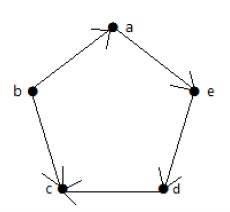
其他頂點的入度和出度如下表所示：

頂點	入度	出度
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1

懸掛頂點

利用頂點的度數，我們有兩種特殊的頂點型別。度數為一的頂點稱為懸掛頂點。

例子

這裡，在這個例子中，頂點“a”和頂點“b”有一條連線邊“ab”。因此，關於頂點“a”，只有一條邊指向頂點“b”，類似地，關於頂點“b”，只有一條邊指向頂點“a”。最後，頂點“a”和頂點“b”的度數為一，也稱為懸掛頂點。

孤立頂點

度數為零的頂點稱為孤立頂點。

例子

這裡，頂點“a”和頂點“b”之間沒有連線，也沒有與任何其他頂點連線。因此，頂點“a”和“b”的度數都為零。這些也稱為孤立頂點。

鄰接

以下是鄰接的規範：

在一個圖中，如果兩個頂點之間有一條邊，則稱這兩個頂點為鄰接的。這裡，頂點的鄰接由連線這兩個頂點的單邊保持。
在一個圖中，如果兩條邊之間有一個公共頂點，則稱這兩條邊為鄰接的。這裡，邊的鄰接由連線兩條邊的單個頂點保持。

示例1

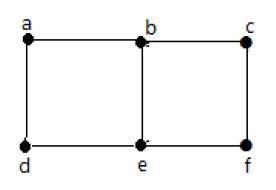
在上圖中：

“a”和“b”是鄰接頂點，因為它們之間有一條公共邊“ab”。
“a”和“d”是鄰接頂點，因為它們之間有一條公共邊“ad”。
“ab”和“be”是鄰接邊，因為它們之間有一個公共頂點“b”。
“be”和“de”是鄰接邊，因為它們之間有一個公共頂點“e”。

示例2

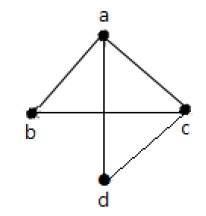
在上圖中：

“a”和“d”是鄰接頂點，因為它們之間有一條公共邊“ad”。
“c”和“b”是鄰接頂點，因為它們之間有一條公共邊“cb”。
“ad”和“cd”是鄰接邊，因為它們之間有一個公共頂點“d”。
“ac”和“cd”是鄰接邊，因為它們之間有一個公共頂點“c”。

平行邊

在一個圖中，如果一對頂點由多於一條邊連線，則這些邊稱為平行邊。

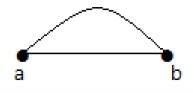
在上圖中，“a”和“b”是兩個頂點，它們之間由兩條邊“ab”和“ab”連線。所以它被稱為平行邊。

多重圖

具有平行邊的圖稱為多重圖。

示例1

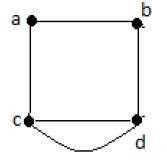
在上圖中，有五條邊“ab”、“ac”、“cd”、“cd”和“bd”。由於“c”和“d”之間有兩條平行邊，它是一個多重圖。

示例2

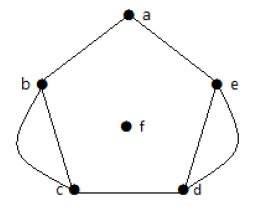
在上圖中，頂點“b”和“c”有兩條邊。頂點“e”和“d”之間也有兩條邊。因此，它是一個多重圖。

圖的度數序列

如果圖中所有頂點的度數按降序或升序排列，則得到的序列稱為該圖的度數序列。

示例1

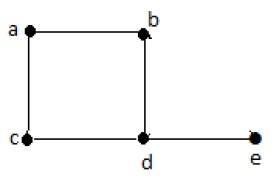
頂點	A	b	c	d	e
連線到	b,c	a,d	a,d	c,b,e	d
度數	2	2	2	3	1

在上圖中，對於頂點{d, a, b, c, e}，度數序列為{3, 2, 2, 2, 1}。

示例2

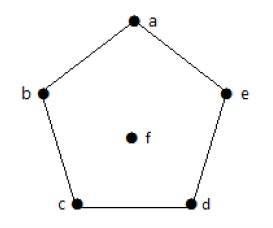
頂點	A	b	c	d	e	f
連線到	b,e	a,c	b,d	c,e	a,d	-
度數	2	2	2	2	2	0

在上圖中，對於頂點{a, b, c, d, e, f}，度數序列為{2, 2, 2, 2, 2, 0}。

圖論 - 基本性質

圖具有各種屬性，這些屬性用於根據圖的結構對圖進行表徵。這些屬性是用圖論領域的相關術語定義的。在本節中，我們將討論一些所有圖中都常見的基本屬性。

兩個頂點之間的距離

這是頂點 U 和頂點 V 之間最短路徑中的邊數。如果有多條路徑連線兩個頂點，則最短路徑被認為是這兩個頂點之間的距離。

符號 − d(U,V)

從一個頂點到另一個頂點可能存在任意數量的路徑。在這些路徑中，您只需要選擇最短的一條。

例子

請看下面的圖：

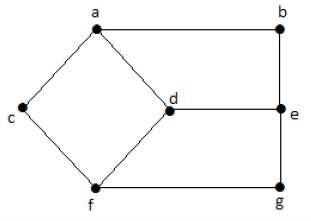
這裡，從頂點“d”到頂點“e”的距離，或簡稱為“de”，是 1，因為它們之間只有一條邊。從頂點“d”到頂點“e”有很多路徑 −

da, ab, be
df, fg, ge
de（它被認為是頂點之間的距離）
df, fc, ca, ab, be
da, ac, cf, fg, ge

頂點的離心率

從一個頂點到所有其他頂點的最大距離被認為是該頂點的離心率。

符號 − e(V)

獲取從特定頂點到圖中所有其他頂點的距離，在這些距離中，離心率是距離中最高的。

例子

在上圖中，“a”的離心率為 3。

從“a”到“b”的距離為 1（'ab'），

從“a”到“c”的距離為 1（'ac'），

從“a”到“d”的距離為 1（'ad'），

從“a”到“e”的距離為 2（'ab'-'be'）或（'ad'-'de'），

從“a”到“f”的距離為 2（'ac'-'cf'）或（'ad'-'df'），

從“a”到“g”的距離為 3（'ac'-'cf'-'fg'）或（'ad'-'df'-'fg'）。

因此，離心率為 3，這是從頂點“a”到距離最長的“ag”的最大值。

換句話說，

e(b) = 3

e(c) = 3

e(d) = 2

e(e) = 3

e(f) = 3

e(g) = 3

連通圖的半徑

所有頂點中的最小離心率被認為是圖 G 的半徑。所有頂點到所有其他頂點的最大距離中的最小值被認為是圖 G 的半徑。

符號 − r(G)

在圖中所有頂點的離心率中，連通圖的半徑是所有這些離心率中的最小值。

例子

在上圖中，r(G) = 2，這是“d”的最小離心率。

圖的直徑

所有頂點中的最大離心率被認為是圖 G 的直徑。所有頂點到所有其他頂點的最大距離被認為是圖 G 的直徑。

**符號 − d(G)** − 在圖中所有頂點的離心率中，連通圖的直徑是所有這些離心率中的最大值。

例子

在上圖中，d(G) = 3；這是最大離心率。

中心點

如果圖的離心率等於其半徑，則它被稱為圖的中心點。如果

e(V) = r(V),

則“V”是圖“G”的中心點。

例子

在示例圖中，“d”是圖的中心點。

e(d) = r(d) = 2

中心

“G”的所有中心點的集合稱為圖的中心。

例子

在示例圖中，{‘d’} 是圖的中心。

周長

**G 的最長迴圈中的邊數** 稱為 G 的周長。

例子

在示例圖中，周長為 6，我們從最長迴圈 a-c-f-g-e-b-a 或 a-c-f-d-e-b-a 推匯出來。

圍長

G 的最短迴圈中的邊數稱為其圍長。

**符號：**g(G)。

**示例** − 在示例圖中，圖的圍長為 4，我們從最短迴圈 a-c-f-d-a 或 d-f-g-e-d 或 a-b-e-d-a 推匯出來。

頂點度數和定理

如果 G = (V, E) 是具有頂點 V = {V₁, V₂,…V_n} 的無向圖，則

n Σ i=1 deg(V_i) = 2|E|

推論 1

如果 G = (V, E) 是具有頂點 V = {V₁, V₂,…V_n} 的有向圖，則

n Σ i=1 deg+(V_i) = |E| = n Σ i=1 deg−(V_i)

推論 2

在任何無向圖中，具有奇數度的頂點數為偶數。

推論 3

在無向圖中，如果每個頂點的度數為 k，則

k|V| = 2|E|

推論 4

在無向圖中，如果每個頂點的度數至少為 k，則

k|V| ≤ 2|E|

| 推論 5

在無向圖中，如果每個頂點的度數最多為 k，則

k|V| ≥ 2|E|

圖論 - 圖的型別

根據頂點數、邊數、互連性和整體結構，存在各種型別的圖。本章只討論幾種重要的圖型別。

空圖

**沒有邊的圖**稱為空圖。

例子

在上圖中，有三個頂點“a”、“b”和“c”，但它們之間沒有邊。因此它是一個空圖。

平凡圖

**只有一個頂點的圖**稱為平凡圖。

例子

在上圖中，只有一個頂點“a”，沒有其他邊。因此它是一個平凡圖。

無向圖

無向圖包含邊，但邊不是有向邊。

例子

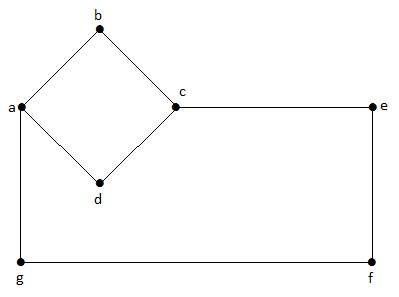
在這個圖中，“a”、“b”、“c”、“d”、“e”、“f”、“g”是頂點，“ab”、“bc”、“cd”、“da”、“ag”、“gf”、“ef”是圖的邊。由於它是一個無向圖，“ab”和“ba”是相同的。其他邊也以相同的方式考慮。

有向圖

在有向圖中，每條邊都有一個方向。

例子

在上圖中，我們有七個頂點“a”、“b”、“c”、“d”、“e”、“f”和“g”，以及八條邊“ab”、“cb”、“dc”、“ad”、“ec”、“fe”、“gf”和“ga”。由於它是有向圖，每條邊都帶有箭頭標記，表示其方向。請注意，在有向圖中，“ab”與“ba”不同。

簡單圖

**沒有環**且沒有**平行邊**的圖稱為簡單圖。

具有“n”個頂點的單個圖中可能的邊數最大為ⁿC₂，其中ⁿC₂ = n(n – 1)/2。
具有“n”個頂點的簡單圖的數量 = 2_ⁿc₂ = 2^n(n-1)/2。

例子

在下圖中，有 3 個頂點和 3 條邊，這是排除平行邊和環的最大值。這可以使用上面的公式來證明。

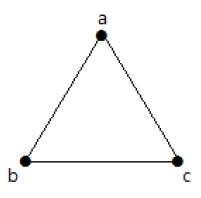
具有 n=3 個頂點的邊數最大 −

ⁿC₂ = n(n–1)/2

= 3(3–1)/2

= 6/2

= 3 條邊

具有 n=3 個頂點的簡單圖的最大數量 −

2_ⁿC₂ = 2^n(n-1)/2

= 2^3(3-1)/2

= 2³

這 8 個圖如下所示 −

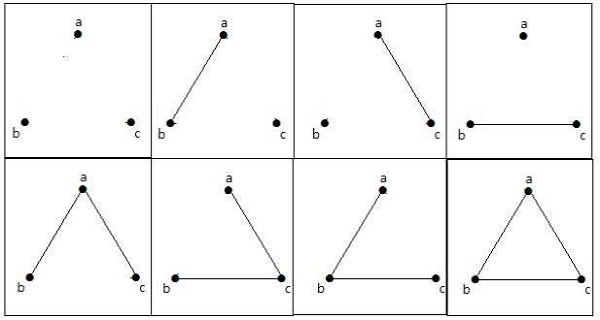
連通圖

如果每對頂點之間都存在一條路徑，則圖 G 被稱為連通圖。圖中每個頂點至少應該有一條邊。這樣我們就可以說它連線到邊的另一側的其他頂點。

例子

在下圖中，每個頂點都有自己的邊連線到另一條邊。因此它是一個連通圖。

非連通圖

如果圖 G 不包含至少兩個連通頂點，則它是斷開的。

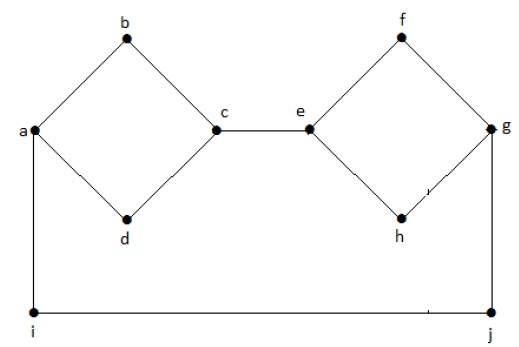
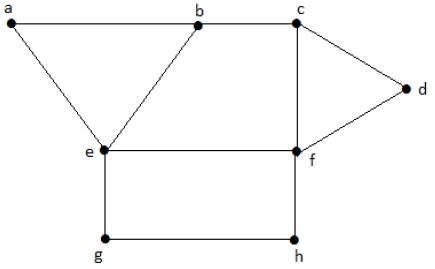
示例1

下圖是非連通圖的一個例子，其中有兩個分量，一個具有“a”、“b”、“c”、“d”頂點，另一個具有“e”、“f”、“g”、“h”頂點。

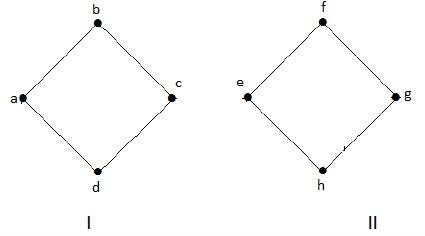
這兩個分量是獨立的，並且彼此不連線。因此它被稱為非連通圖。

示例2

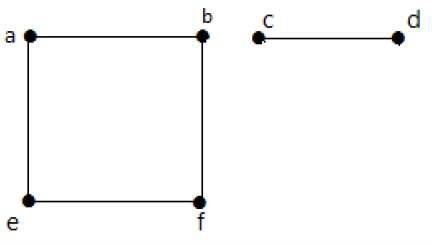
在這個例子中，有兩個獨立的分量，a-b-f-e 和 c-d，它們彼此不相連。因此這是一個非連通圖。

正則圖

如果圖 G 的所有頂點具有相同的度數，則稱圖 G 為正則圖。如果圖中每個頂點的度數為“k”，則該圖稱為“k-正則圖”。

例子

在下圖中，所有頂點都具有相同的度數。因此這些圖被稱為正則圖。

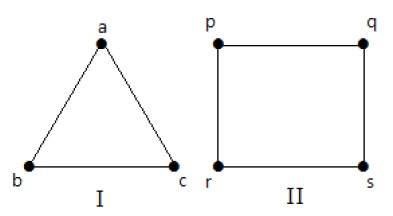
在這兩個圖中，所有頂點的度數都是 2。它們被稱為 2-正則圖。

完全圖

具有“n”個互連頂點的簡單圖稱為完全圖，並用“K_n”表示。在圖中，**一個頂點應該與所有其他頂點都有邊連線**，則稱為完全圖。

換句話說，如果一個頂點連線到圖中的所有其他頂點，則它被稱為完全圖。

例子

在下圖中，圖中的每個頂點都與圖中的所有其他頂點連線，但自身除外。

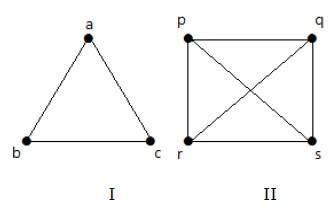
在圖 I 中，

	a	b	c
a	未連線	已連線	已連線
b	已連線	未連線	已連線
c	已連線	已連線	未連線

在圖 II 中，

	p	q	r	s
p	未連線	已連線	已連線	已連線
q	已連線	未連線	已連線	已連線
r	已連線	已連線	未連線	已連線
s	已連線	已連線	已連線	未連線

環圖

具有“n”個頂點（n >= 3）和“n”條邊的簡單圖，如果其所有邊形成長度為“n”的環，則稱為環圖。

如果圖中每個頂點的度數為二，則它被稱為環圖。

**符號** − C_n

例子

看一下下面的圖 −

圖 I 有 3 個頂點和 3 條邊，形成環“ab-bc-ca”。
圖 II 有 4 個頂點和 4 條邊，形成環“pq-qs-sr-rp”。
圖 III 有 5 個頂點和 5 條邊，形成環“ik-km-ml-lj-ji”。

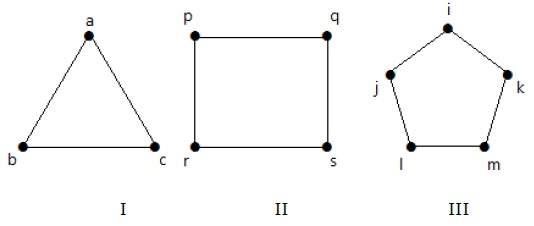
因此，所有給定的圖都是環圖。

輪圖

透過新增一個新頂點從環圖 C_n-1 獲得輪圖。這個新頂點稱為**中心**，它與 C_n 的所有頂點相連。

符號 − W_n

W_n 中的邊數 = 中心到所有其他頂點的邊數 +

環圖中所有其他節點（無中心）的邊數。

= (n–1) + (n–1)

= 2(n–1)

例子

看一下下面的圖。它們都是輪圖。

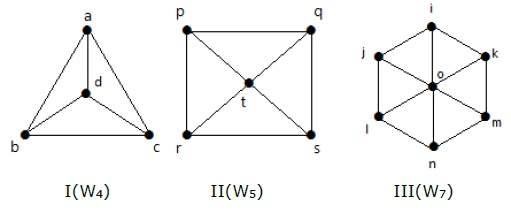
在圖 I 中，它是透過在中間新增一個名為“d”的頂點從 C₃ 獲得的。它表示為 W₄。

W4 中的邊數 = 2(n-1) = 2(3) = 6

在圖 II 中，它是透過在中間新增一個名為“t”的頂點從 C4 獲得的。它表示為 W₅。

W5 中的邊數 = 2(n-1) = 2(4) = 8

圖 III 是由 C₆ 新增一個名為“o”的中間頂點得到的。它表示為 W₇。

W₄ 中邊的數量 = 2(n-1) = 2(6) = 12

迴圈圖

至少包含一個環的圖稱為迴圈圖。

例子

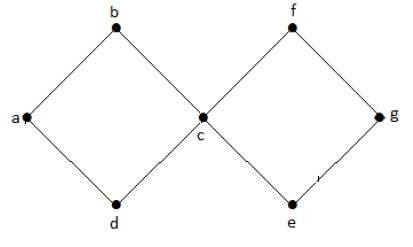
在上例圖中，我們有兩個環 a-b-c-d-a 和 c-f-g-e-c。因此它被稱為迴圈圖。

無環圖

沒有環的圖稱為無環圖。

例子

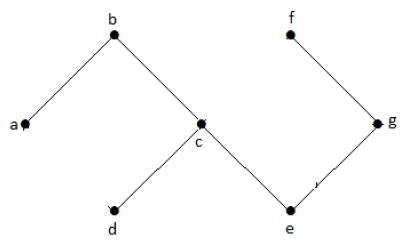
在上例圖中，我們沒有任何環。因此它是一個無環圖。

二分圖

頂點劃分 V = {V₁, V₂} 的簡單圖 G = (V, E) 如果**E 的每條邊都連線 V₁ 中的一個頂點和 V₂ 中的一個頂點**，則稱為二分圖。

一般來說，二分圖有兩個頂點集，例如 V₁ 和 V₂，如果畫一條邊，它應該連線 V₁ 集中的任何頂點到 V₂ 集中的任何頂點。

例子

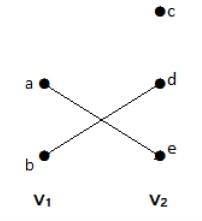
在這個圖中，您可以觀察到兩組頂點——V₁ 和 V₂。這裡，名為“ae”和“bd”的兩條邊連線著 V₁ 和 V₂ 兩組的頂點。

完全二分圖

如果劃分 V = {V₁, V₂} 的二分圖“G”，G = (V, E) 中 V₁ 的每個頂點都連線到 V₂ 的每個頂點，則稱其為完全二分圖。

一般來說，完全二分圖連線 V₁ 集中的每個頂點到 V₂ 集中的每個頂點。

例子

下圖是一個完全二分圖，因為它有連線 V₁ 集中每個頂點到 V₂ 集中每個頂點的邊。

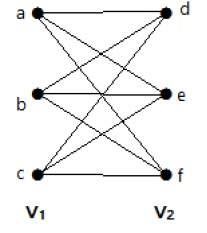
如果 |V₁| = m 且 |V₂| = n，則完全二分圖表示為 K_{m, n}。

K_m,n 有 (m+n) 個頂點和 (mn) 條邊。
如果 m=n，則 K_m,n 是一個正則圖。

一般來說，**完全二分圖不是完全圖**。

如果 m=n=1，則 K_m,n 是一個完全圖。

具有 n 個頂點的二分圖中邊的最大數量為：

[n²/4]

如果 n=10，k_{5, 5} = [n²/4] = [10²/4] = 25。

同樣，K_{6, 4}=24

K_{7, 3}=21

K_{8, 2}=16

K_{9, 1}=9

如果 n=9，k_{5, 4} = [n²/4] = [9²/4] = 20

同樣，K_{6, 3}=18

K_{7, 2}=14

K_{8, 1}=8

如果“G”沒有奇數長度的環，“G”就是一個二分圖。二分圖的一個特例是星形圖。

星形圖

形式為 K_{1, n-1} 的完全二分圖是一個具有 n 個頂點的星形圖。如果單個頂點屬於一個集合，而所有剩餘頂點屬於另一個集合，則星形圖是完全二分圖。

例子

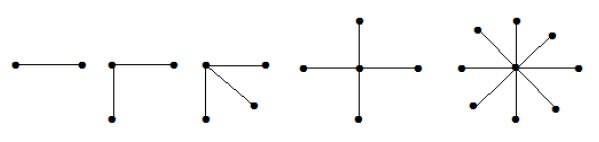
在上圖中，“n”個頂點中，所有“n-1”個頂點都連線到單個頂點。因此，它具有 K¹, ^n-1 的形式，它們是星形圖。

圖的補圖

設“G−”是一個簡單圖，其頂點與“G”相同，如果邊{U, V}不存在於 G 中，則邊{U, V}存在於“G−”中。這意味著，如果兩個頂點在 G 中不相鄰，則它們在“G−”中相鄰。

如果圖 I 中存在的邊在另一個圖 II 中不存在，並且如果圖 I 和圖 II 組合在一起形成一個完全圖，則圖 I 和圖 II 互稱為補圖。

例子

在下面的例子中，圖 I 有兩條邊“cd”和“bd”。其補圖 II 有四條邊。

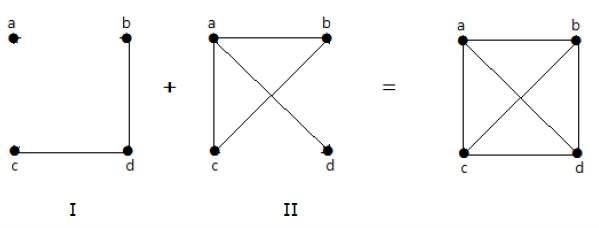
請注意，圖 I 中的邊不存在於圖 II 中，反之亦然。因此，兩圖的組合給出了“n”個頂點的完全圖。

**注意**——兩個補圖的組合構成一個完全圖。

如果“G”是任何簡單圖，則

|E(G)| + |E('G-')| = |E(K_n)|，其中 n = 圖中頂點的數量。

例子

設“G”是一個具有九個頂點和十二條邊的簡單圖，求“G−”中的邊數。

你有，|E(G)| + |E('G-')| = |E(K_n)|

12 + |E('G-')| =

9(9-1) / 2 = ⁹C₂

12 + |E('G-')| = 36

|E('G-')| = 24

“G”是一個具有 40 條邊和其補圖“G−”具有 38 條邊的簡單圖。求圖 G 或“G−”中的頂點數。

設圖中頂點的數量為“n”。

我們有，|E(G)| + |E('G-')| = |E(K_n)|

40 + 38 = n(n-1)/2

78 = n(n-1)/2

156 = n(n-1)

13 × 12 = n(n-1)

圖論 - 樹

樹是即使不包含單個環的圖。它們以圖形形式表示分層結構。樹屬於最簡單的圖類。儘管它們很簡單，但它們具有豐富的結構。

樹提供了一系列有用的應用程式，從簡單的家譜到計算機科學資料結構中的樹。

樹

**連通的無環圖**稱為樹。換句話說，沒有環的連通圖稱為樹。

樹的邊稱為**分支**。樹的元素稱為其節點。沒有子節點的節點稱為**葉節點**。

具有“n”個頂點的樹具有“n-1”條邊。如果它比“n-1”多一條邊，則額外的邊顯然必須與兩個頂點配對，從而形成一個環。然後，它變成一個迴圈圖，這違反了樹圖的規定。

示例1

此處顯示的圖是一棵樹，因為它沒有環並且是連通的。它有四個頂點和三條邊，即對於“n”個頂點“n-1”條邊，如定義中所述。

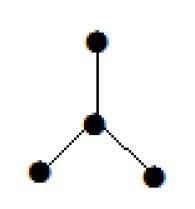
**注意**——每棵樹至少有兩個度數為一的頂點。

示例2

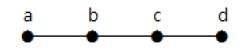
在上例中，頂點“a”和“d”的度數為一。其他兩個頂點“b”和“c”的度數為二。這是可能的，因為為了不形成環，圖中至少應該有兩個單邊。它只不過是兩個度數為一的邊。

森林

**不連通的無環圖**稱為森林。換句話說，樹的不相交集合稱為森林。

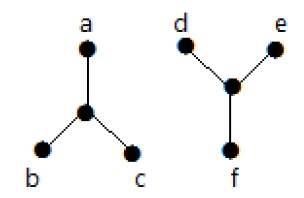
例子

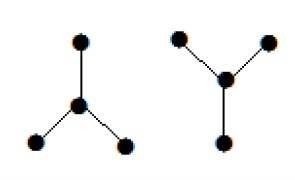
下圖看起來像兩個子圖；但它是一個單一的不連通圖。此圖中沒有環。因此，它顯然是一個森林。

生成樹

設 G 為連通圖，則 G 的子圖 H 稱為 G 的生成樹，如果：

H 是一棵樹
H 包含 G 的所有頂點。

無向圖 G 的生成樹 T 是包含 G 所有頂點的子圖。

例子

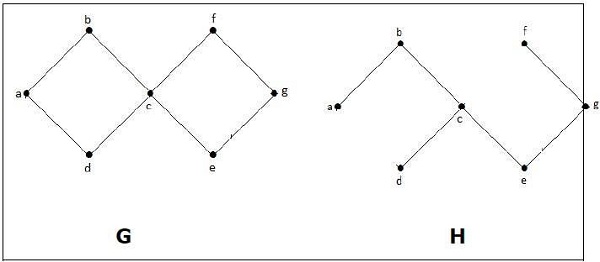
在上例中，G 是連通圖，H 是 G 的子圖。

顯然，圖 H 沒有環，它是一棵具有六條邊的樹，比頂點總數少一條。因此，H 是 G 的生成樹。

迴路秩

設“G”是具有“n”個頂點和“m”條邊的連通圖。“G”的生成樹“T”包含 (n-1) 條邊。

因此，為了得到生成樹，你需要從“G”中刪除的邊數 = m-(n-1)，這稱為 G 的迴路秩。

這個公式是正確的，因為在生成樹中，你需要有“n-1”條邊。在“m”條邊中，你需要在圖中保留“n-1”條邊。

因此，從“m”中刪除“n-1”條邊得到為了獲得不應形成環的生成樹而需要從圖中刪除的邊。

例子

請看下面的圖：

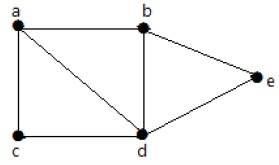
對於上例中給出的圖，你有 m=7 條邊和 n=5 個頂點。

則迴路秩為：

G = m – (n – 1)

= 7 – (5 – 1) = 3

= 3

例子

設“G”是一個具有六個頂點且每個頂點的度數為三的連通圖。求“G”的迴路秩。

根據頂點度數之和定理：

**n Σ i=1** deg(V_i) = 2|E|

6 × 3 = 2|E|

|E| = 9

迴路秩 = |E| – (|V| – 1)

= 9 – (6 – 1) = 4

基爾霍夫定理

基爾霍夫定理可用於查詢可以從連通圖中形成的生成樹的數量。

例子

矩陣“A”填充如下：如果兩個頂點之間存在邊，則應將其指定為“1”，否則為“0”。

$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$

使用基爾霍夫定理，應將其更改為將主對角線值替換為頂點的度數，並將所有其他元素替換為 -1.A

$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$M_{11}的餘子式= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$

因此，生成樹的數量 = 8。

圖論 - 連通性

是否可以從一個頂點遍歷到另一個頂點取決於圖的連線方式。連通性是圖論中的一個基本概念。連通性定義了圖是連通的還是不連通的。它根據邊和頂點有子主題，稱為邊連通性和頂點連通性。讓我們詳細討論它們。

連通性

如果每對頂點之間都存在一條路徑，則稱圖是**連通的**。從每個頂點到任何其他頂點，都應該有一些路徑可供遍歷。這稱為圖的連通性。具有多個不連通頂點和邊的圖稱為不連通圖。

示例1

在下圖中，可以從一個頂點遍歷到任何其他頂點。例如，可以使用路徑“a-b-e”從頂點“a”遍歷到頂點“e”。

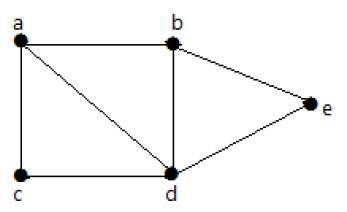
示例2

在下面的例子中，無法從頂點“a”遍歷到頂點“f”，因為它們之間沒有直接或間接的路徑。因此它是一個不連通圖。

割頂

設“G”是一個連通圖。如果“G-V”（從“G”中刪除“V”）導致不連通圖，則頂點 V ∈ G 稱為“G”的割頂。從圖中移除割頂會將其分成兩個或多個圖。

**注意**——移除割頂可能會使圖不連通。

連通圖“G”最多可能有 (n-2) 個割頂。

例子

在下圖中，頂點“e”和“c”是割頂。

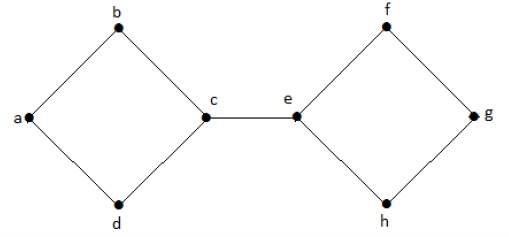
透過移除“e”或“c”，圖將變成不連通圖。

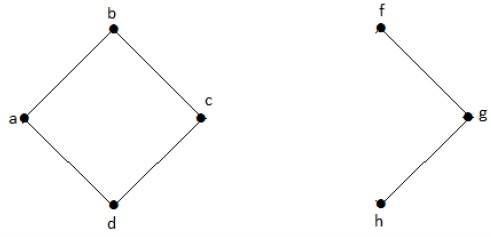
沒有“g”，頂點“c”和頂點“h”以及許多其他頂點之間沒有路徑。因此它是一個不連通圖，其割頂為“e”。同樣，“c”也是上圖的割頂。

割邊（橋）

設“G”是一個連通圖。如果“G-e”導致不連通圖，則邊“e”∈ G 稱為割邊。

如果移除圖中的一條邊會導致兩個或多個圖，則該邊稱為割邊。

例子

在下圖中，割邊是 [(c, e)]。

透過從圖中移除邊 (c, e)，它變成了不連通圖。

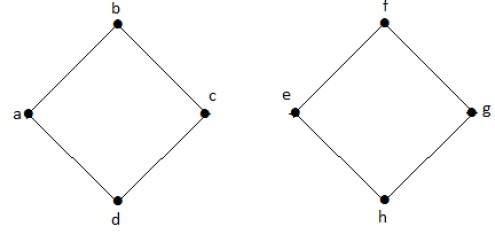
在上圖中，移除邊 (c, e) 將圖分成兩個，這實際上是一個不連通圖。因此，邊 (c, e) 是該圖的割邊。

**注意**——設“G”是一個具有“n”個頂點的連通圖，則

邊“e”∈ G 是割邊當且僅當邊“e”不是 G 中任何環的一部分。
可能的割邊最大數量為“n-1”。
只要存在割邊，就一定存在割頂，因為至少割邊的一個頂點是割頂。
如果存在割頂，則割邊可能存在也可能不存在。

圖的割集

設‘G’=(V, E)是一個連通圖。E 的子集 E’ 稱為 G 的割集，如果從 G 中刪除 E’ 中的所有邊會使 G 不連通。

如果從圖中刪除一定數量的邊使其不連通，則這些被刪除的邊稱為該圖的割集。

例子

看下面的圖。它的割集是 E1 = {e1, e3, e5, e8}。

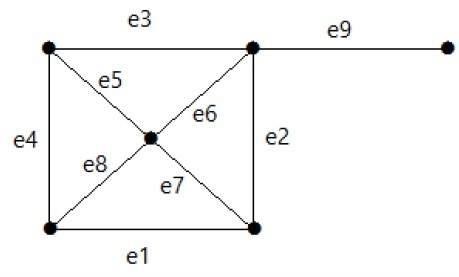
從圖中移除割集 E1 後，圖將如下所示：

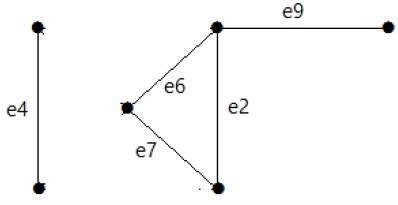
同樣，還有其他可以使圖不連通的割集：

E3 = {e9} – 圖中最小的割集。
E4 = {e3, e4, e5}

邊連通度

設‘G’是一個連通圖。刪除最少數量的邊使得‘G’不連通的邊的數量稱為 G 的邊連通度。

符號 − λ(G)

換句話說，G 的最小割集中邊的數量稱為 G 的邊連通度。

如果‘G’有一條割邊，則 λ(G) 為 1。（G 的邊連通度。）

例子

看下面的圖。透過移除兩條最小邊，連通圖變得不連通。因此，它的邊連通度 (λ(G)) 為 2。

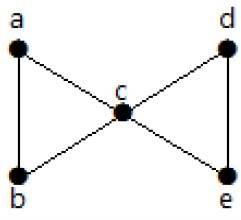
以下是透過移除兩條邊使圖不連通的四種方法：

點連通度

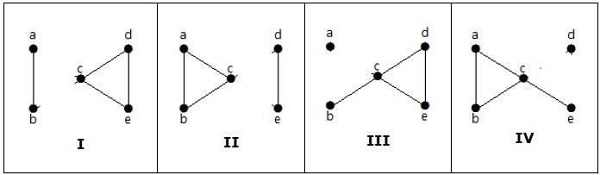
設‘G’是一個連通圖。刪除最少數量的頂點使得‘G’不連通或將‘G’簡化為平凡圖的頂點數稱為它的點連通度。

符號 − K(G)

例子

在上圖中，移除頂點‘e’和‘i’使圖不連通。

如果 G 有一個割頂，則 K(G) = 1。

符號 − 對於任何連通圖 G，

K(G) ≤ λ(G) ≤ δ(G)

點連通度 (K(G))，邊連通度 (λ(G))，G 的最小度數 (δ(G))。

例子

計算下列圖的 λ(G) 和 K(G)：

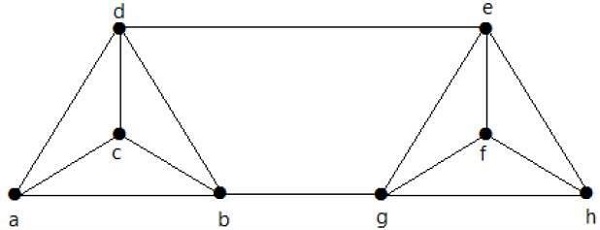
解答

從圖中，

δ(G) = 3

K(G) ≤ λ(G) ≤ δ(G) = 3 (1)

K(G) ≥ 2 (2)

刪除邊 {d, e} 和 {b, h}，我們可以使 G 不連通。

因此，

λ(G) = 2

2 ≤ λ(G) ≤ δ(G) = 2 (3)

從 (2) 和 (3)，點連通度 K(G) = 2

圖論 - 覆蓋

覆蓋圖是一個子圖，它包含所有頂點或與某個其他圖對應的所有邊。包含所有頂點的子圖稱為線/邊覆蓋。包含所有邊的子圖稱為點覆蓋。

線覆蓋

設 G = (V, E) 為一個圖。C(E) 的一個子集稱為 G 的線覆蓋，如果 G 的每個頂點都至少與 C 中的一條邊關聯，即

deg(V) ≥ 1 ∀ V ∈ G

因為每個頂點都透過一條邊與另一個頂點相連。因此它至少有 1 度。

例子

請看下面的圖：

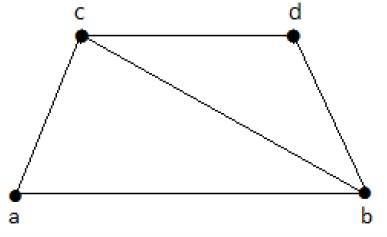
其具有線覆蓋的子圖如下：

C₁ = {{a, b}, {c, d}}

C₂ = {{a, d}, {b, c}}

C₃ = {{a, b}, {b, c}, {b, d}}

C₄ = {{a, b}, {b, c}, {c, d}}

當且僅當‘G’有一個孤立頂點時，‘G’不存線上覆蓋。具有‘n’個頂點的圖的線覆蓋至少有 [n/2] 條邊。

最小線覆蓋

如果不能從 C 中刪除任何邊，則圖 G 的線覆蓋 C 稱為最小線覆蓋。

例子

在上圖中，具有線覆蓋的子圖如下：

C₁ = {{a, b}, {c, d}}

C₂ = {{a, d}, {b, c}}

C₃ = {{a, b}, {b, c}, {b, d}}

C₄ = {{a, b}, {b, c}, {c, d}}

這裡，C₁、C₂、C₃是最小線覆蓋，而 C₄ 不是，因為我們可以刪除 {b, c}。

最小線覆蓋

也稱為最小最小線覆蓋。具有最少邊數的最小線覆蓋稱為‘G’的最小線覆蓋。‘G’的最小線覆蓋中的邊數稱為‘G’的線覆蓋數 (α₁)。

例子

在上面的例子中，C₁和 C₂是 G 的最小線覆蓋，並且 α₁ = 2。

每個線覆蓋都包含一個最小線覆蓋。
並非每個線覆蓋都包含一個最小線覆蓋（C₃不包含任何最小線覆蓋）。
任何最小線覆蓋都不包含環。
如果線覆蓋‘C’不包含長度為 3 或更長的路徑，則‘C’是最小線覆蓋，因為‘C’的所有分量都是星圖，並且從星圖中不能刪除任何邊。

點覆蓋

設‘G’ = (V, E) 為一個圖。V 的子集 K 稱為‘G’的點覆蓋，如果‘G’的每條邊都與 K 中的一個頂點關聯或被 K 中的一個頂點覆蓋。

例子

請看下面的圖：

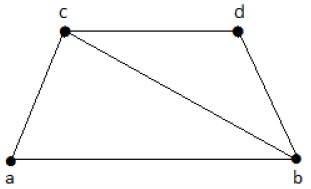
可以從上圖匯出的子圖如下：

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

K₄ = {a, d}

這裡，K₁、K₂和 K₃具有點覆蓋，而 K₄沒有任何點覆蓋，因為它沒有覆蓋邊 {bc}。

最小點覆蓋

如果不能從‘K’中刪除任何頂點，則圖‘G’的頂點‘K’稱為最小點覆蓋。

例子

在上圖中，具有點覆蓋的子圖如下：

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

這裡，K₁和 K₂是最小點覆蓋，而在 K₃中，可以刪除頂點‘d’。

最小點覆蓋

也稱為最小最小點覆蓋。具有最少頂點數的圖‘G’的最小點覆蓋稱為最小點覆蓋。

‘G’的最小點覆蓋中的頂點數稱為 G 的點覆蓋數 (α₂)。

例子

在下圖中，具有點覆蓋的子圖如下：

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

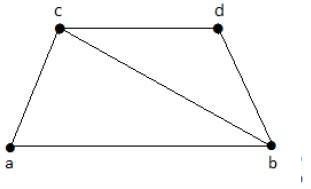
這裡，K₁是 G 的最小點覆蓋，因為它只有兩個頂點。α₂ = 2。

圖論 - 匹配

匹配圖是一個圖的子圖，其中沒有邊彼此相鄰。簡單地說，任何兩條邊之間都不應有任何公共頂點。

匹配

設‘G’ = (V, E) 為一個圖。如果G 的每個頂點最多與 M 中的一條邊關聯，則子圖稱為匹配 M(G)，即

deg(V) ≤ 1 ∀ V ∈ G

這意味著在匹配圖 M(G) 中，頂點的度數應為 1 或 0，其中邊應來自圖 G。

符號 − M(G)

例子

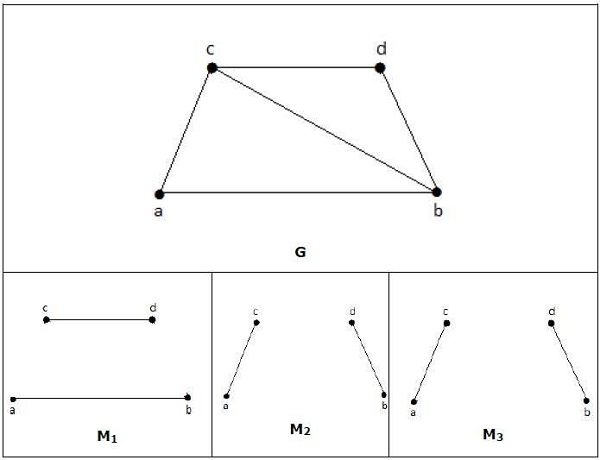
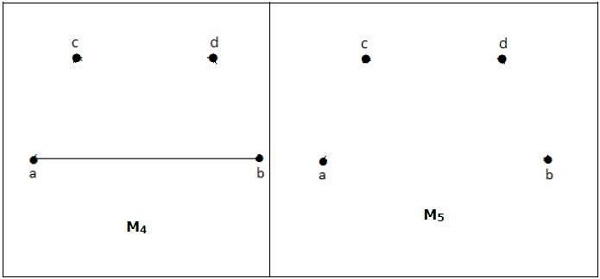
在匹配中，

如果 deg(V) = 1，則 (V) 被稱為匹配的

如果 deg(V) = 0，則 (V) 沒有匹配。

在匹配中，沒有兩條邊是相鄰的。這是因為如果任何兩條邊相鄰，則連線這兩條邊的頂點的度數將為 2，這違反了匹配規則。

極大匹配

如果不能將‘G’的其他邊新增到 M，則圖‘G’的匹配 M 稱為極大匹配。

例子

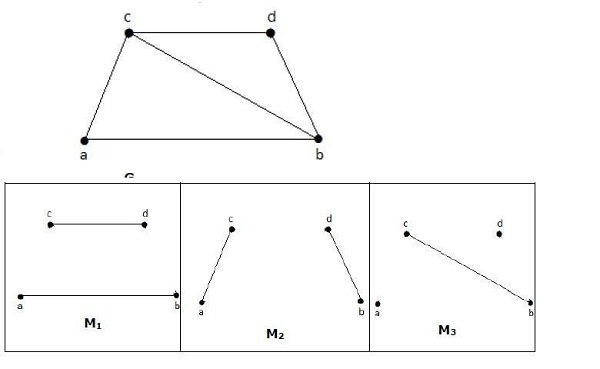
上圖中的 M1、M2、M3 是 G 的極大匹配。

最大匹配

也稱為最大極大匹配。最大匹配定義為具有最大邊數的極大匹配。

‘G’的最大匹配中的邊數稱為其匹配數。

例子

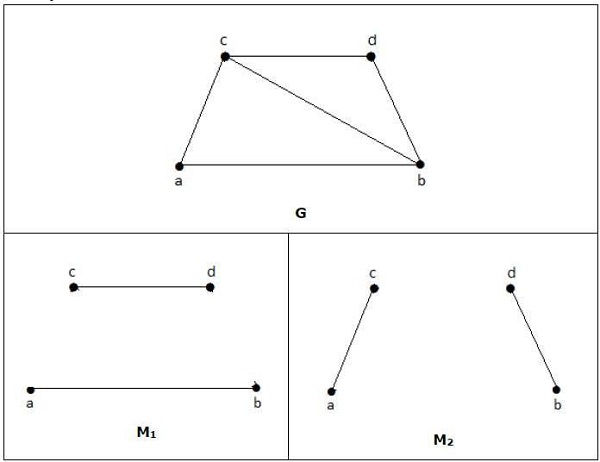
對於上面例子中給出的圖，M1 和 M2 是‘G’的最大匹配，其匹配數為 2。因此，使用圖 G，我們最多隻能形成只有 2 條邊的子圖。因此，匹配數為 2。

完美匹配

如果圖 g (G) 的每個頂點都恰好與匹配 (M) 的一條邊關聯，則圖 (G) 的匹配 (M) 稱為完美匹配，即

deg(V) = 1 ∀ V

子圖中每個頂點的度數都應為 1。

例子

在下圖中，M1 和 M2 是 G 的完美匹配的例子。

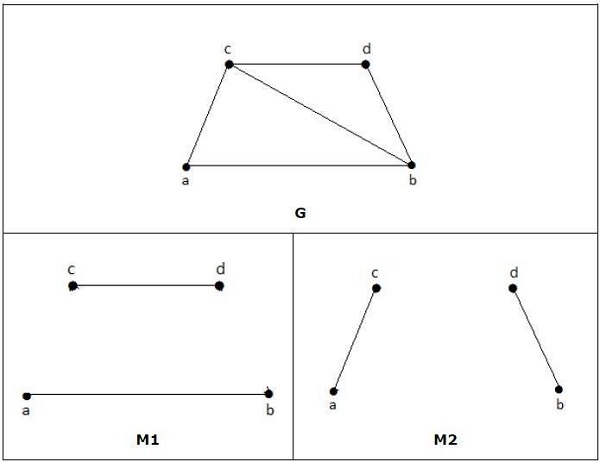
注意 − 圖的每個完美匹配也是圖的最大匹配，因為在完美匹配圖中不可能再新增一條邊。

圖的最大匹配不必是完美的。如果圖‘G’有一個完美匹配，則頂點數 |V(G)| 為偶數。如果它是奇數，則最後一個頂點與另一個頂點配對，最終剩下一個單個頂點，它不能與任何其他頂點配對，其度數為零。這顯然違反了完美匹配原則。

例子

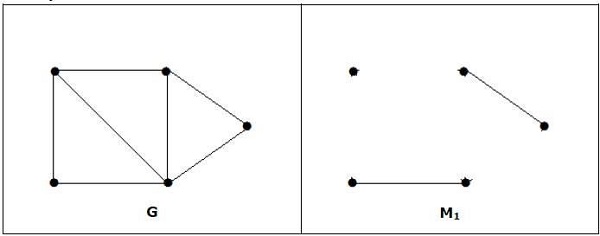
注意 − 上述語句的反面不一定為真。如果 G 具有偶數個頂點，則 M1 不必是完美的。

例子

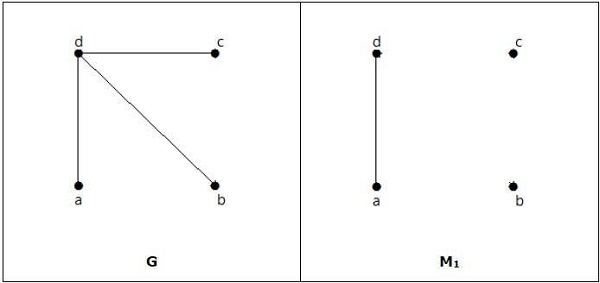
它是匹配，但它不是完美匹配，即使它有偶數個頂點。

圖論 - 獨立集

獨立集用集合表示，其中

不應有任何彼此相鄰的邊。任何兩條邊之間都不應有任何公共頂點。
不應有任何彼此相鄰的頂點。任何兩個頂點之間都不應有任何公共邊。

獨立線集

設‘G’ = (V, E) 為一個圖。E 的子集 L 稱為‘G’的獨立線集，如果 L 中的任何兩條邊都不相鄰。這樣的集合稱為獨立線集。

例子

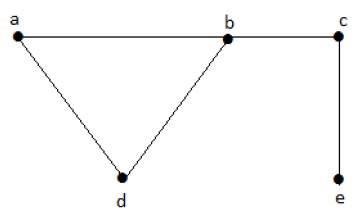
讓我們考慮以下子集：

L₁ = {a,b}
L₂ = {a,b} {c,e}
L₃ = {a,d} {b,c}

在這個例子中，子集 L2 和 L3 明顯不是給定圖中的相鄰邊。它們是獨立線集。但是 L1 不是獨立線集，因為要構成獨立線集，至少應該有兩條邊。

極大獨立線集

如果不能將‘G’的其他邊新增到‘L’，則獨立線集稱為圖‘G’的極大獨立線集。

例子

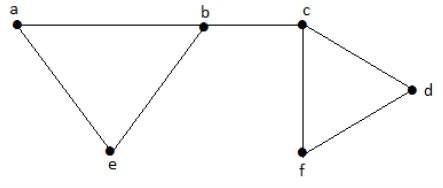
讓我們考慮以下子集：

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L₂和 L₃是極大獨立線集/極大匹配。因為只有對於這兩個子集，沒有機會新增任何非相鄰的邊。因此，這兩個子集被認為是極大獨立線集。

最大獨立線集

具有最大邊數的‘G’的最大獨立線集稱為‘G’的最大獨立線集。

Number of edges in a maximum independent line set of G (β₁)
   = Line independent number of G
   = Matching number of G

例子

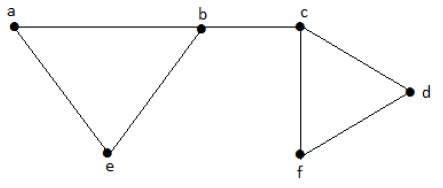
讓我們考慮以下子集：

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L₃是 G 的最大獨立線集，具有圖中不相鄰的最大邊數，記作 β1 = 3。

注意 − 對於任何沒有孤立頂點的圖 G，

α1 + β1 = 圖中的頂點數 = |V|

例子

K_n/C_n/w_n 的線覆蓋數，

$$α 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:如果\:n\:是偶數 \\\frac{n+1}{2}\:如果\:n\:是奇數\end{cases}$$

獨立線數（匹配數）= β₁ = [n/2] α₁ + β₁ = n。

獨立頂點集

設‘G’ = (V, E) 為一個圖。如果‘S’中沒有兩個頂點相鄰，則‘V’的一個子集稱為‘G’的獨立集。

例子

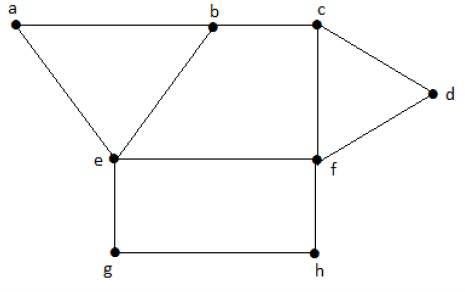
考慮上圖中的以下子集：

S₁ = {e}

S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

顯然，S₁不是一個獨立頂點集，因為要得到一個獨立頂點集，圖中至少應該有兩個頂點。但這裡並非如此。子集S₂、S₃和S₄是獨立頂點集，因為沒有一個頂點與子集中的任何一個頂點相鄰。

最大獨立頂點集

設“G”是一個圖，則當“G”的任何其他頂點都不能新增到“S”中時，“G”的獨立頂點集被稱為最大獨立頂點集。

例子

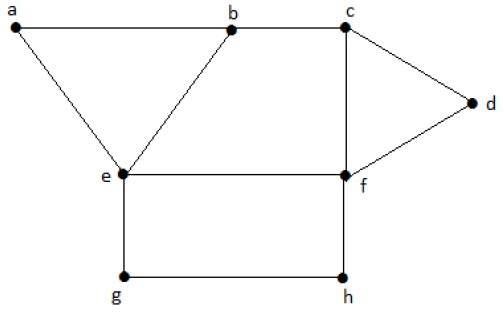
考慮上述圖中的以下子集。

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

S₂和S₃是“G”的最大獨立頂點集。在S₁和S₄中，我們可以新增其他頂點；但在S₂和S₃中，我們不能新增任何其他頂點。

最大獨立頂點集

具有最大頂點數的“G”的最大獨立頂點集稱為最大獨立頂點集。

例子

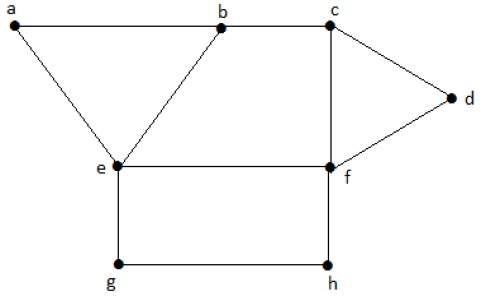
考慮上述圖中的以下子集：

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

只有S₃是最大獨立頂點集，因為它包含最多的頂點。 “G”的最大獨立頂點集中的頂點數稱為G的獨立頂點數 (β₂)。

例子

對於完全圖K_n，

頂點覆蓋數 = α₂ = n−1

頂點獨立數 = β₂ = 1

α₂ + β₂ = n

在一個完全圖中，每個頂點與其剩餘的 (n − 1) 個頂點相鄰。因此，K_n的最大獨立集只包含一個頂點。

因此，β₂=1

且α₂=|v| − β₂ = n-1

注意 − 對於任何圖“G” = (V, E)

α₂ + β₂ = |v|
如果“S”是“G”的獨立頂點集，則 (V – S) 是G的頂點覆蓋。

圖論 - 著色

圖著色只不過是在某些約束下對圖元件（例如頂點、邊和區域）進行標記的一種簡單方法。在一個圖中，沒有兩個相鄰的頂點、相鄰的邊或相鄰的區域用最少的顏色著色。這個數字稱為色數，該圖稱為正確著色的圖。

在圖著色中，對圖設定的約束包括顏色、著色順序、顏色分配方式等。顏色賦予頂點或特定區域。因此，具有相同顏色的頂點或區域形成獨立集。

頂點著色

頂點著色是將顏色分配給圖“G”的頂點，以使任何兩個相鄰頂點都不具有相同的顏色。簡而言之，邊的兩個頂點不應具有相同的顏色。

色數

圖“G”頂點著色所需的最小顏色數稱為G的色數，記為X(G)。

當且僅當'G'是空圖時，χ(G) = 1。如果'G'不是空圖，則χ(G) ≥ 2。

例子

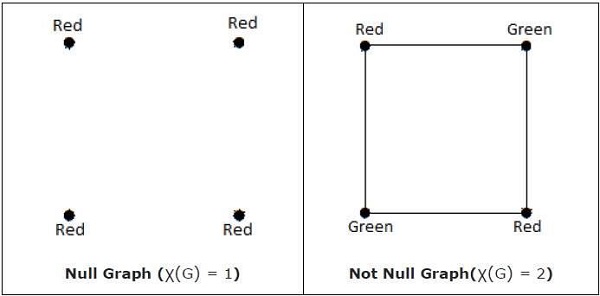
注意 − 如果存在一個最多使用n種顏色的頂點著色，則稱圖“G”是n可著色的，即X(G) ≤ n。

區域著色

區域著色是將顏色分配給平面圖的區域，以使任何兩個相鄰區域都不具有相同的顏色。如果兩個區域具有公共邊，則稱它們為相鄰區域。

例子

看一下下面的圖。區域“aeb”和“befc”是相鄰的，因為這兩個區域之間有公共邊“be”。

類似地，其他區域也根據鄰接關係著色。此圖著色如下：

例子

Kn的色數是

n
n–1
[n/2]
[n/2]

考慮K₄的這個例子。

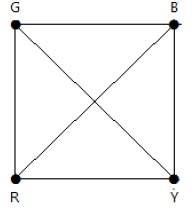
在完全圖中，每個頂點與其剩餘的 (n – 1) 個頂點相鄰。因此，每個頂點都需要一種新顏色。因此，K_n的色數 = n。

圖著色的應用

圖著色是圖論中最重要的概念之一。它用於計算機科學的許多即時應用中，例如：

聚類
資料探勘
影像採集
影像分割
網路
資源分配
程序排程

圖論 - 同構

圖可以以不同的形式存在，具有相同的頂點數、邊數以及相同的邊連通性。這樣的圖稱為同構圖。請注意，本章中我們主要為了參考和區分這些圖而對它們進行標記。

同構圖

如果滿足以下條件，則兩個圖G₁和G₂被稱為同構：

它們的元件數（頂點和邊）相同。
它們的邊連通性保持不變。

注意 − 簡而言之，在兩個同構圖中，一個圖是另一個圖的修改版本。未標記的圖也可以被認為是同構圖。

There exists a function ‘f’ from vertices of G₁ to vertices of G₂
   [f: V(G₁) ⇒ V(G₂)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G₁, then the
edge {f(U), f(V)} ∈ G₂, then G₁ ≡ G₂.

注意

如果G₁ ≡ G₂，則：

|V(G₁)| = |V(G₂)|

|E(G₁)| = |E(G₂)|

G₁和G₂的度數序列相同。

如果頂點 {V₁, V₂, .. Vk} 在G₁中形成長度為K的環，則頂點 {f(V₁), f(V₂),… f(Vk)} 應在G₂中形成長度為K的環。

所有上述條件對於圖G₁和G₂是同構的都是必要的，但不足以證明這些圖是同構的。

(G₁ ≡ G₂) 當且僅當 (G₁− ≡ G₂−)，其中G₁和G₂是簡單圖。
(G₁ ≡ G₂) 如果G₁和G₂的鄰接矩陣相同。
(G₁ ≡ G₂) 當且僅當G₁和G₂的對應子圖（透過刪除G1中的一些頂點及其在圖G₂中的映象獲得）是同構的。

例子

以下哪些圖是同構的？

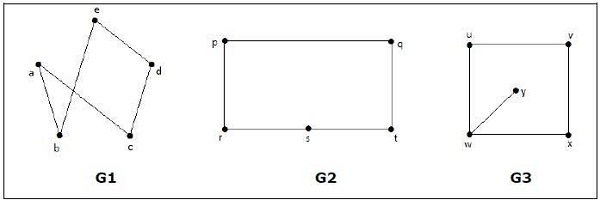
在圖G₃中，頂點“w”的度數只有3，而所有其他圖頂點的度數都為2。因此，G3與G₁或G₂不同構。

取G₁和G₂的補圖，我們有：

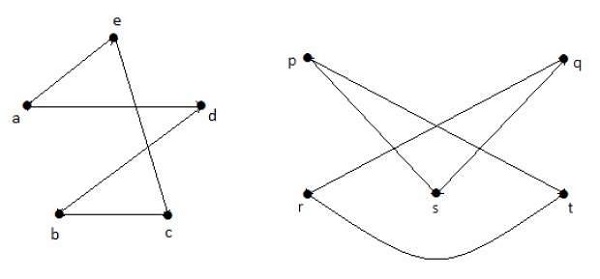
這裡，(G₁− ≡ G₂−)，因此 (G₁ ≡ G₂)。

平面圖

如果一個圖“G”可以在平面上或球面上繪製，使得沒有兩條邊在非頂點處相交，則稱該圖“G”為平面圖。

例子

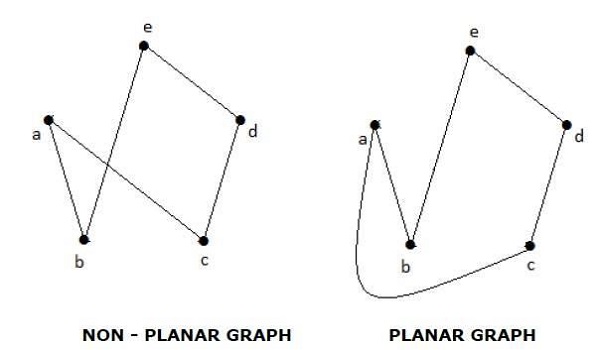
區域

每個平面圖都將平面劃分為稱為區域的連通區域。

例子

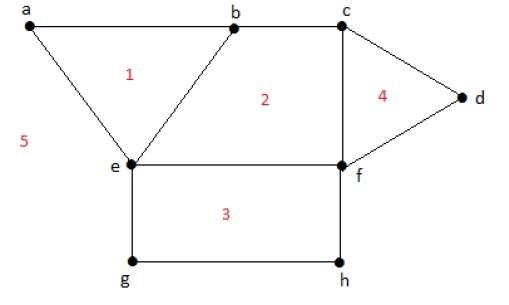
有界區域的度數r = deg(r) = 包圍區域r的邊的數量。

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8

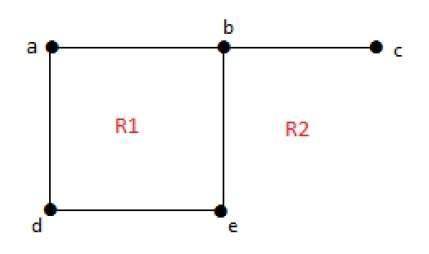
無界區域的度數r = deg(r) = 包圍區域r的邊的數量。

deg(R₁) = 4
deg(R₂) = 6

在平面圖中，以下性質成立：

在一個具有“n”個頂點的平面圖中，所有頂點的度數之和為：

n Σ i=1 deg(V_i) = 2|E|

根據區域度數之和/定理，在一個具有“n”個區域的平面圖中，區域度數之和為：

n Σ i=1 deg(ri) = 2|E|

基於上述定理，您可以得出以下結論：

在一個平面圖中，

如果每個區域的度數為K，則區域度數之和為：

K|R| = 2|E|

如果每個區域的度數至少為K(≥ K)，則

K|R| ≤ 2|E|

如果每個區域的度數最多為K(≤ K)，則

K|R| ≥ 2|E|

注意 − 假設所有區域的度數相同。

根據平面圖上的尤拉公式，

如果一個圖“G”是連通平面圖，則

|V| + |R| = |E| + 2

如果一個平面圖有“K”個分量，則

|V| + |R|=|E| + (K+1)

其中，|V| 是頂點數，|E| 是邊數，|R| 是區域數。

邊頂點不等式

如果“G”是一個連通平面圖，每個區域的度數至少為“K”，則

|E| ≤ k / (k-2) {|v| - 2}

我們知道，|V| + |R| = |E| + 2

K.|R| ≤ 2|E|

K(|E| - |V| + 2) ≤ 2|E|

(K - 2)|E| ≤ K(|V| - 2)

|E| ≤ k / (k-2) {|v| - 2}

如果“G”是一個簡單的連通平面圖，則

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

至少存在一個頂點 V •∈ G，使得 deg(V) ≤ 5。

如果“G”是一個簡單的連通平面圖（至少有2條邊）且沒有三角形，則

|E| ≤ {2|V| – 4}

庫拉托夫斯基定理

一個圖“G”是非平面的當且僅當“G”具有一個與K₅或K_3,3同胚的子圖。

同胚

如果可以透過用更多頂點劃分G的一些邊從同一個圖“G”獲得這兩個圖中的每一個，則稱兩個圖G₁和G₂是同胚的。看下面的例子：

透過新增一個頂點將邊“rs”分成兩條邊。

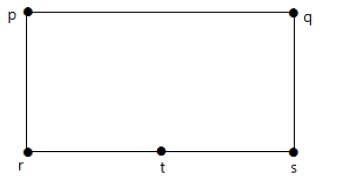
下面顯示的圖與第一個圖同胚。

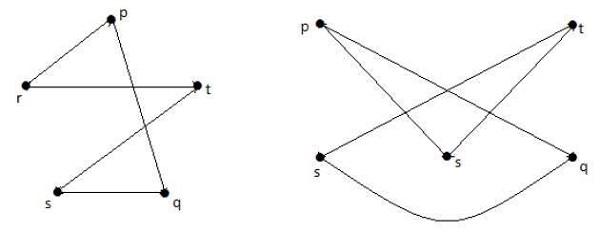
如果G₁與G₂同構，則G與G2同胚，但反過來不一定成立。

任何具有4個或更少頂點的圖都是平面圖。
任何具有8條或更少邊的圖都是平面圖。
完全圖K_n是平面圖當且僅當n ≤ 4。
完全二部圖K_{m, n}是平面圖當且僅當m ≤ 2或n ≤ 2。
具有最小頂點數的簡單非平面圖是完全圖K₅。
具有最小邊數的簡單非平面圖是K_{3, 3}。

多面體圖

如果每個頂點的度數≥ 3，即deg(V) ≥ 3 ∀ V ∈ G，則稱簡單的連通平面圖為多面體圖。

3|V| ≤ 2|E|
3|R| ≤ 2|E|

圖論 - 可遍歷性

如果您可以繪製一條路徑連線所有頂點而無需回溯同一條路徑，則該圖是可遍歷的。基於此路徑，本章中描述了一些類別，例如尤拉路徑和歐拉回路。

尤拉路徑

尤拉路徑恰好包含“G”的每條邊一次，並且至少包含“G”的每個頂點一次。如果連通圖G包含尤拉路徑，則稱該圖是可遍歷的。

例子

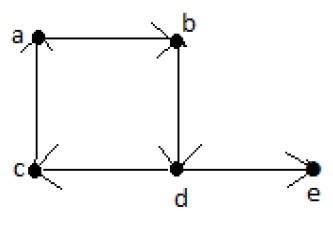
尤拉路徑 = d-c-a-b-d-e。

歐拉回路

在尤拉路徑中，如果起點與終點相同，則稱為歐拉回路。

例子

尤拉路徑 = a-b-c-d-a-g-f-e-c-a。

歐拉回路定理

一個連通圖“G”是可遍歷的當且僅當G中具有奇數度的頂點數恰好為2或0。如果一個連通圖G恰好有兩個奇數度頂點，則它可以包含尤拉路徑，但不能包含歐拉回路。

注意 − 此尤拉路徑以奇數度頂點開始，以另一個奇數度頂點結束。

例子

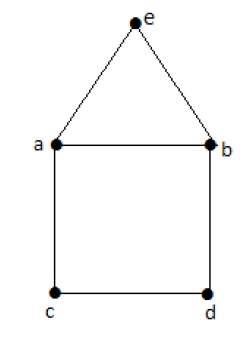
尤拉路徑 − b-e-a-b-d-c-a 不是歐拉回路，但它是尤拉路徑。顯然它恰好有兩個奇數度頂點。

注意 − 在連通圖G中，如果具有奇數度的頂點數 = 0，則存在歐拉回路。

哈密頓圖

如果存在一個包含G的所有頂點的環，則稱連通圖G為哈密頓圖。

每個環都是迴路，但迴路可能包含多個環。這樣的環稱為G的哈密頓環。

哈密頓路徑

如果一個連通圖恰好包含G的每個頂點一次，則稱該圖是哈密頓圖。這樣的路徑稱為哈密頓路徑。

例子

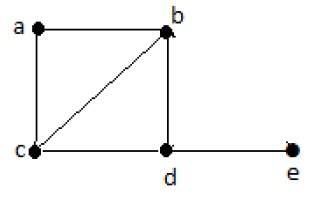
哈密頓路徑− e-d-b-a-c。

注意

歐拉回路恰好包含圖的每條邊一次。
在哈密頓環中，可以跳過圖的某些邊。

例子

請看下面的圖：

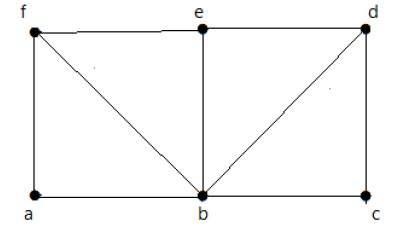
對於上面顯示的圖：

存在尤拉路徑 – 否
存在歐拉回路 – 否
存在哈密頓環 – 是
存在哈密頓路徑 – 正確

G 有四個奇數度頂點，因此它不可遍歷。透過跳過內部邊，該圖具有一個經過所有頂點的哈密頓環。

圖論 - 例子

本章將介紹一些標準示例，以演示我們在前面章節中已經討論過的概念。

示例1

求下列圖中生成樹的個數。

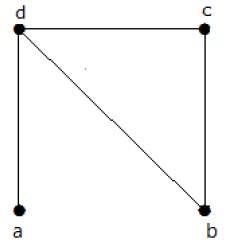
解答

從上圖獲得的生成樹個數為 3。它們如下所示：

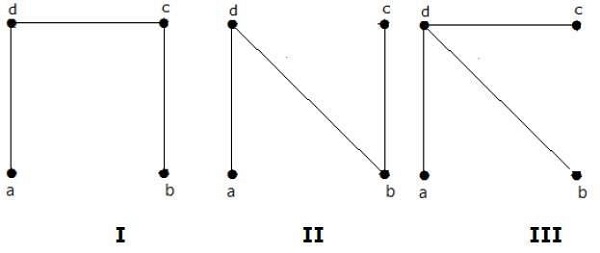
這三個是給定圖的生成樹。這裡圖 I 和圖 II 彼此同構。顯然，非同構生成樹的個數為兩個。

示例2

用 3 個頂點可以構成多少個簡單的非同構圖？

解答

用 3 個頂點可以構成 4 個非同構圖。它們如下所示。

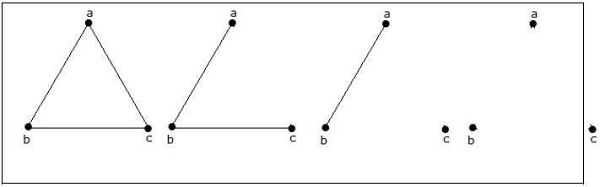
例 3

設‘G’是一個具有 20 個頂點的連通平面圖，每個頂點的度數為 3。求該圖中區域的個數。

解答

根據度數和定理，

20 Σ i=1 deg(Vi) = 2|E|

20(3) = 2|E|

|E| = 30

根據尤拉公式，

|V| + |R| = |E| + 2

20+ |R| = 30 + 2

|R| = 12

因此，區域個數為 12。

例 4

完全圖 K_n 的色數是多少？

解答

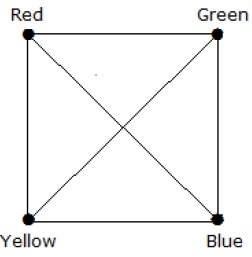
在完全圖中，每個頂點都與其餘 (n–1) 個頂點相鄰。因此，每個頂點都需要一種新的顏色。因此，完全圖 K_n 的色數 = n。

例 5

下列圖的匹配數是多少？

解答

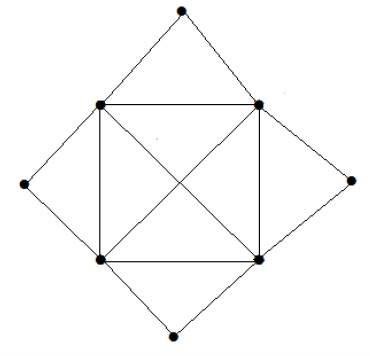
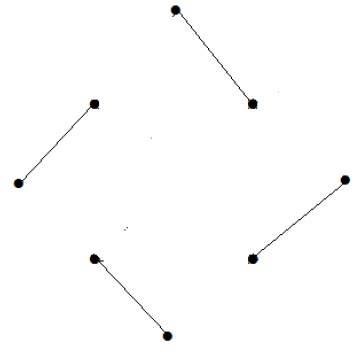
頂點數 = 9

我們只能匹配 8 個頂點。

匹配數為 4。

例 6

下列圖的邊覆蓋數是多少？

解答

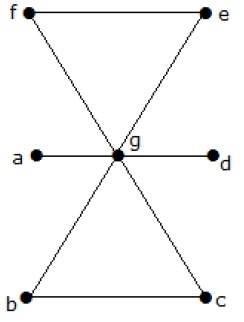
頂點數 = |V| = n = 7

邊覆蓋數 = (α₁) ≥ [n/2] = 3

α₁ ≥ 3

使用 3 條邊，我們可以覆蓋所有頂點。

因此，邊覆蓋數為 3。

列印頁面