圖論 - 例子

---

---

在本章中，我們將介紹一些標準示例，以演示我們在前面章節中已經討論的概念。

示例 1

求以下圖中生成樹的個數。

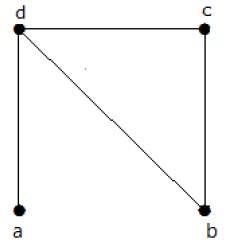
解答

從上圖得到的生成樹個數為 3。它們如下所示：

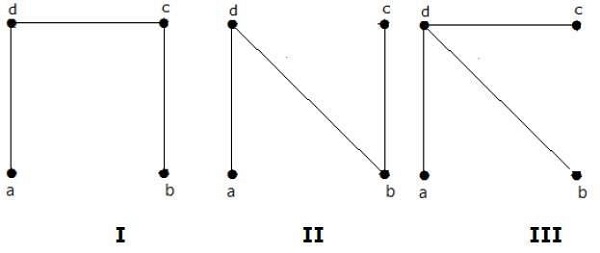
這三個是給定圖的生成樹。這裡圖 I 和 II 彼此同構。顯然，非同構生成樹的個數為兩個。

示例 2

3 個頂點可能有多少個簡單的非同構圖？

解答

3 個頂點可能存在 4 個非同構圖。它們如下所示。

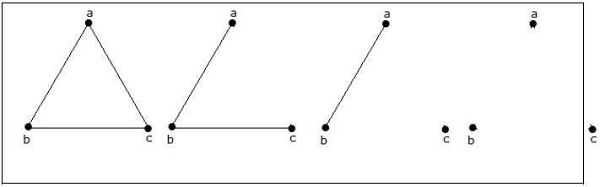
示例 3

設“G”是一個具有 20 個頂點的連通平面圖，每個頂點的度數為 3。求圖中區域的個數。

解答

根據度數和定理，

20 Σ i=1 deg(Vi) = 2|E|

20(3) = 2|E|

|E| = 30

根據尤拉公式，

|V| + |R| = |E| + 2

20+ |R| = 30 + 2

|R| = 12

因此，區域的個數為 12。

示例 4

完全圖 K_n 的色數是多少？

解答

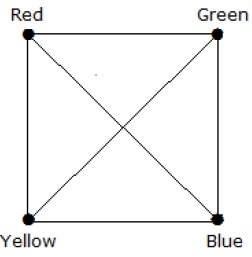
在完全圖中，每個頂點都與其餘 (n–1) 個頂點相鄰。因此，每個頂點都需要一個新的顏色。因此，完全圖 K_n 的色數為 n。

示例 5

以下圖的匹配數是多少？

解答

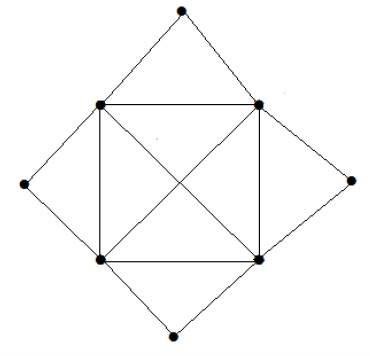
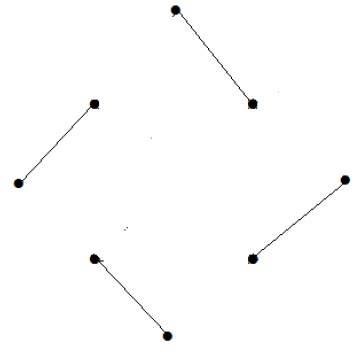
頂點數 = 9

我們只能匹配 8 個頂點。

匹配數為 4。

示例 6

以下圖的邊覆蓋數是多少？

解答

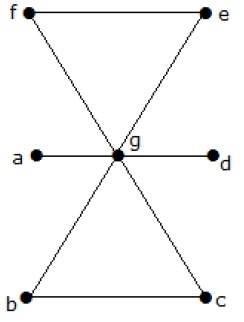
頂點數 = |V| = n = 7

邊覆蓋數 = (α₁) ≥ [n/2] = 3

α₁ ≥ 3

使用 3 條邊，我們可以覆蓋所有頂點。

因此，邊覆蓋數為 3。