
圖論 - 基礎知識
圖是由點和連線這些點的線組成的圖表。它至少有一條線連線一組兩個頂點,並且沒有頂點連線自身。圖論中的圖的概念建立在一些基本術語之上,例如點、線、頂點、邊、頂點的度數、圖的性質等。在本章中,我們將介紹這些圖論的基礎知識。
點
點是一維、二維或三維空間中的特定位置。為了更好地理解,可以用字母表示一個點。它可以用一個點來表示。
示例

這裡,點是一個名為“a”的點。
線
線是連線兩點的連線。它可以用實線表示。
示例

這裡,“a”和“b”是點。這兩點之間的連線稱為線。
頂點
頂點是多條線相交的點。它也稱為節點。與點類似,頂點也用字母表示。
示例

這裡,頂點用字母“a”命名。
邊
邊是連線兩個頂點的線的數學術語。從單個頂點可以形成許多邊。沒有頂點,就不能形成邊。邊必須有一個起始頂點和一個結束頂點。
示例

這裡,“a”和“b”是兩個頂點,它們之間的連線稱為邊。
圖
圖“G”定義為 G = (V, E),其中 V 是圖中所有頂點的集合,E 是圖中所有邊的集合。
示例 1
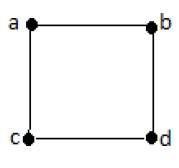
在上例中,ab、ac、cd 和 bd 是圖的邊。類似地,a、b、c 和 d 是圖的頂點。
示例 2
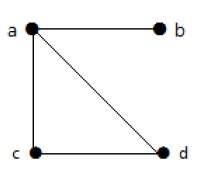
在這個圖中,有四個頂點 a、b、c 和 d,以及四條邊 ab、ac、ad 和 cd。
環
在圖中,如果從頂點到自身畫一條邊,則稱為環。
示例 1

在上圖中,V 是一個頂點,它有一條邊 (V, V) 形成一個環。
示例 2

在這個圖中,頂點 a 和頂點 b 各形成兩個環。
頂點的度數
它是與頂點 V 相鄰的頂點數。
符號 − deg(V)。
在一個具有 n 個頂點的簡單圖中,任何頂點的度數為 −
deg(v) ≤ n – 1 ∀ v ∈ G
一個頂點可以與所有其他頂點形成邊,但不能與自身形成邊。因此,頂點的度數最多為圖中頂點數減 1。這個 1 是指自身頂點,因為它不能自己形成環。如果任何頂點都有環,則它不是簡單圖。
頂點的度數可以考慮圖的兩種情況 −
無向圖
有向圖
無向圖中頂點的度數
無向圖沒有有向邊。考慮以下示例。
示例 1
看一下下面的圖 −
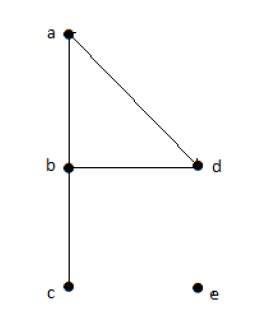
在上圖中,
deg(a) = 2,因為頂點“a”上有 2 條邊相交。
deg(b) = 3,因為頂點“b”上有 3 條邊相交。
deg(c) = 1,因為頂點“c”上形成 1 條邊
所以“c”是懸掛頂點。
deg(d) = 2,因為頂點“d”上有 2 條邊相交。
deg(e) = 0,因為頂點“e”上沒有形成邊。
所以“e”是孤立頂點。
示例 2
看一下下面的圖 −
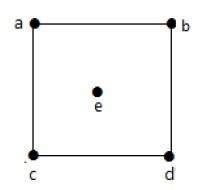
在上圖中,
deg(a) = 2,deg(b) = 2,deg(c) = 2,deg(d) = 2,deg(e) = 0。
頂點“e”是孤立頂點。該圖沒有任何懸掛頂點。
有向圖中頂點的度數
在有向圖中,每個頂點都有一個入度和一個出度。
圖的入度
頂點 V 的入度是進入頂點 V 的邊的數量。
符號 − deg−(V)。
圖的出度
頂點 V 的出度是從頂點 V 出發的邊的數量。
符號 − deg+(V)。
考慮以下示例。
示例 1
看一下下面的有向圖。頂點“a”有兩條邊,“ad”和“ab”,它們向外延伸。因此,它的出度為 2。類似地,有一條邊“ga”指向頂點“a”。因此,“a”的入度為 1。
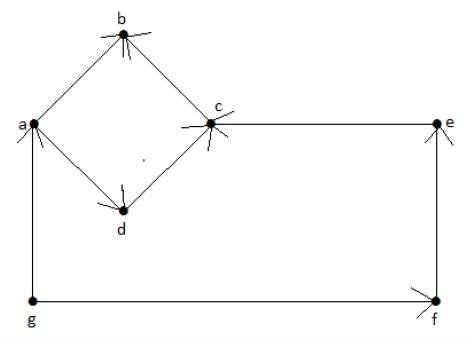
其他頂點的入度和出度如下表所示 −
| 頂點 | 入度 | 出度 |
|---|---|---|
| a | 1 | 2 |
| b | 2 | 0 |
| c | 2 | 1 |
| d | 1 | 1 |
| e | 1 | 1 |
| f | 1 | 1 |
| g | 0 | 2 |
示例 2
看一下下面的有向圖。頂點“a”有一條邊“ae”從頂點“a”向外延伸。因此,它的出度為 1。類似地,該圖有一條邊“ba”指向頂點“a”。因此,“a”的入度為 1。
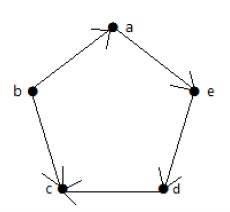
其他頂點的入度和出度如下表所示 −
| 頂點 | 入度 | 出度 |
|---|---|---|
| a | 1 | 1 |
| b | 0 | 2 |
| c | 2 | 0 |
| d | 1 | 1 |
| e | 1 | 1 |
懸掛頂點
利用頂點的度數,我們有兩個特殊的頂點型別。度數為一的頂點稱為懸掛頂點。
示例

在這個例子中,頂點“a”和頂點“b”有一條連線邊“ab”。因此,關於頂點“a”,只有一條邊指向頂點“b”,類似地,關於頂點“b”,只有一條邊指向頂點“a”。最後,頂點“a”和頂點“b”的度數為 1,也稱為懸掛頂點。
孤立頂點
度數為零的頂點稱為孤立頂點。
示例

這裡,頂點“a”和頂點“b”彼此之間以及與任何其他頂點之間都沒有連線。因此,頂點“a”和“b”的度數都為零。這些也稱為孤立頂點。
鄰接
以下是鄰接的規範 −
在一個圖中,如果兩個頂點之間有一條邊,則稱這兩個頂點鄰接。這裡,頂點的鄰接由連線這兩個頂點的單邊來維持。
在一個圖中,如果兩條邊之間有一個公共頂點,則稱這兩條邊鄰接。這裡,邊的鄰接由連線兩條邊的單個頂點來維持。
示例 1
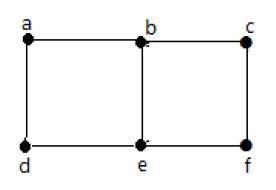
在上圖中 −
“a”和“b”是鄰接頂點,因為它們之間有一條公共邊“ab”。
“a”和“d”是鄰接頂點,因為它們之間有一條公共邊“ad”。
“ab”和“be”是鄰接邊,因為它們之間有一個公共頂點“b”。
“be”和“de”是鄰接邊,因為它們之間有一個公共頂點“e”。
示例 2
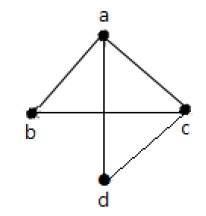
在上圖中 −
“a”和“d”是鄰接頂點,因為它們之間有一條公共邊“ad”。
“c”和“b”是鄰接頂點,因為它們之間有一條公共邊“cb”。
“ad”和“cd”是鄰接邊,因為它們之間有一個公共頂點“d”。
“ac”和“cd”是鄰接邊,因為它們之間有一個公共頂點“c”。
平行邊
在一個圖中,如果一對頂點由多於一條邊連線,則這些邊稱為平行邊。
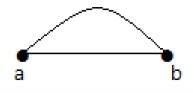
在上圖中,“a”和“b”是兩個頂點,它們之間由兩條邊“ab”和“ab”連線。因此,它被稱為平行邊。
多重圖
具有平行邊的圖稱為多重圖。
示例 1
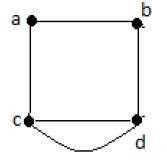
在上圖中,有五條邊“ab”、“ac”、“cd”、“cd”和“bd”。由於“c”和“d”之間有兩條平行邊,所以它是一個多重圖。
示例 2
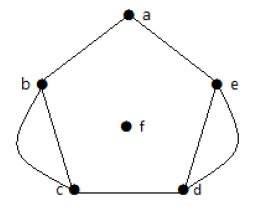
在上圖中,頂點“b”和“c”有兩條邊。頂點“e”和“d”之間也有兩條邊。因此,它是一個多重圖。
圖的度數序列
如果圖中所有頂點的度數按降序或升序排列,則得到的序列稱為圖的度數序列。
示例 1
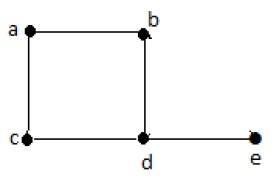
| 頂點 | A | b | c | d | e |
|---|---|---|---|---|---|
| 連線到 | b,c | a,d | a,d | c,b,e | d |
| 度數 | 2 | 2 | 2 | 3 | 1 |
在上圖中,對於頂點 {d, a, b, c, e},度數序列為 {3, 2, 2, 2, 1}。
示例 2
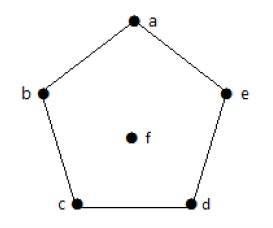
| 頂點 | A | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 連線到 | b,e | a,c | b,d | c,e | a,d | - |
| 度數 | 2 | 2 | 2 | 2 | 2 | 0 |
在上圖中,對於頂點 {a, b, c, d, e, f},度數序列為 {2, 2, 2, 2, 2, 0}。