
圖論 - 獨立集
獨立集用集合表示,其中
不應該有**任何彼此相鄰的邊**。任何兩條邊之間不應該有公共頂點。
不應該有**任何彼此相鄰的頂點**。任何兩個頂點之間不應該有公共邊。
獨立線集
設“G” = (V, E) 為一個圖。E 的一個子集 L 稱為“G”的獨立線集,如果 L 中的任何兩條邊都不相鄰。這樣的集合稱為獨立線集。
例子
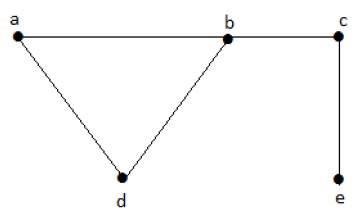
讓我們考慮以下子集 -
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}
在這個例子中,子集 L2 和 L3 明顯不是給定圖中的相鄰邊。它們是獨立線集。但是 L1 不是獨立線集,因為要構成獨立線集,至少需要兩條邊。
最大獨立線集
如果圖“G”的任何其他邊都不能新增到“L”,則稱獨立線集為圖“G”的最大獨立線集。
例子
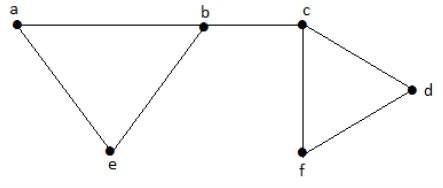
讓我們考慮以下子集 -
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}
L2 和 L3 是最大獨立線集/最大匹配。因為只有對於這兩個子集,才沒有機會新增任何其他不相鄰的邊。因此,這兩個子集被認為是最大獨立線集。
最大獨立線集
具有最大邊數的“G”的最大獨立線集稱為“G”的最大獨立線集。
Number of edges in a maximum independent line set of G (β1) = Line independent number of G = Matching number of G
例子
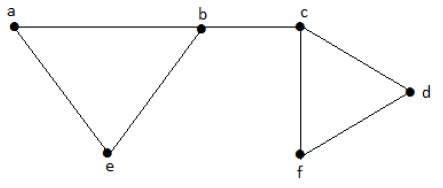
讓我們考慮以下子集 -
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}
L3 是 G 的最大獨立線集,它具有最多的不相鄰邊,表示為 β1 = 3。
注意 - 對於任何沒有孤立頂點的圖 G,
α1 + β1 = 圖中頂點數 = |V|
例子
Kn/Cn/wn 的線覆蓋數,
$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:如果\:n\:是偶數 \\\frac{n+1}{2}\:如果\:n\:是奇數\end{cases}$$線獨立數(匹配數)= β1 = [n/2] α1 + β1 = n。
獨立頂點集
設“G” = (V, E) 為一個圖。“V”的一個子集稱為“G”的獨立集,如果“S”中的任何兩個頂點都不相鄰。
例子
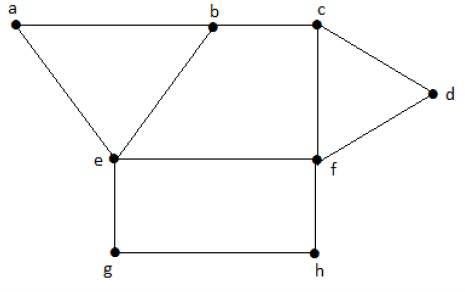
考慮上面圖中以下子集 -
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}
顯然 S1 不是一個獨立頂點集,因為要獲得一個獨立頂點集,圖中至少需要兩個頂點。但這裡情況並非如此。子集 S2、S3 和 S4 是獨立頂點集,因為沒有一個頂點與子集中的任何一個頂點相鄰。
最大獨立頂點集
設“G”為一個圖,則“G”的一個獨立頂點集被稱為最大獨立頂點集,如果“G”的任何其他頂點都不能新增到“S”。
例子
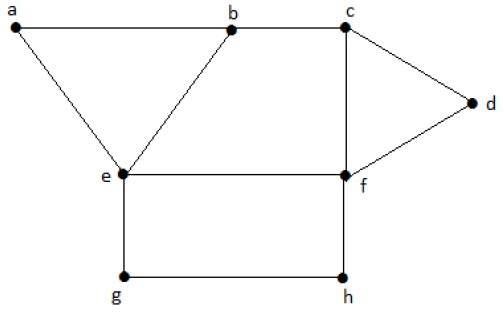
考慮上面圖中以下子集。
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}
S2 和 S3 是“G”的最大獨立頂點集。在 S1 和 S4 中,我們可以新增其他頂點;但在 S2 和 S3 中,我們不能新增任何其他頂點。
最大獨立頂點集
具有最大頂點數的“G”的最大獨立頂點集稱為最大獨立頂點集。
例子
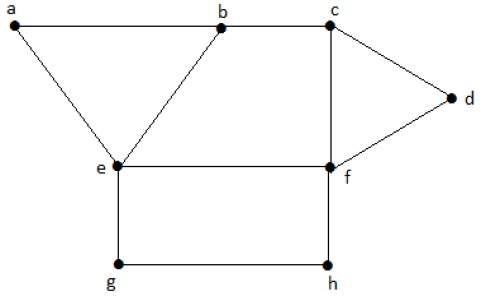
考慮上面圖中以下子集 -
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}
只有 S3 是最大獨立頂點集,因為它覆蓋了最多的頂點。“G”的最大獨立頂點集中的頂點數稱為 G 的獨立頂點數 (β2)。
例子
對於完全圖 Kn,
頂點覆蓋數 = α2 = n−1
頂點獨立數 = β2 = 1
你有 α2 + β2 = n
在一個完全圖中,每個頂點都與其剩餘的 (n − 1) 個頂點相鄰。因此,Kn 的最大獨立集只包含一個頂點。
因此,β2=1
並且 α2=|v| − β2 = n-1
注意 - 對於任何圖“G” = (V, E)
- α2 + β2 = |v|
- 如果“S”是“G”的一個獨立頂點集,則 (V – S) 是 G 的頂點覆蓋。