
圖論 - 基本性質
圖具有各種屬性,這些屬性用於根據圖的結構對其進行表徵。這些屬性以與圖論領域相關的特定術語定義。在本章中,我們將討論一些所有圖中都常見的基本屬性。
兩個頂點之間的距離
它是頂點 U 和頂點 V 之間最短路徑上的邊數。如果有多條路徑連線兩個頂點,則最短路徑被視為這兩個頂點之間的距離。
符號 - d(U,V)
從一個頂點到另一個頂點可能存在任意數量的路徑。在其中,您只需要選擇最短的一條。
例子
看一下下面的圖 -
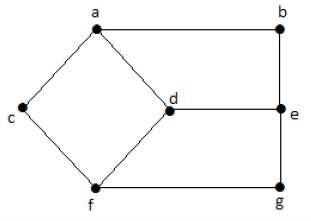
這裡,從頂點“d”到頂點“e”或簡稱為“de”的距離為 1,因為它們之間有一條邊。從頂點“d”到頂點“e”有很多路徑 -
- da, ab, be
- df, fg, ge
- de(它被認為是頂點之間的距離)
- df, fc, ca, ab, be
- da, ac, cf, fg, ge
頂點的離心率
從一個頂點到所有其他頂點的最大距離被認為是該頂點的離心率。
符號 - e(V)
取從特定頂點到圖中所有其他頂點的距離,在這些距離中,離心率是距離中最高的。
例子
在上圖中,“a”的離心率為 3。
從“a”到“b”的距離為 1('ab'),
從“a”到“c”的距離為 1('ac'),
從“a”到“d”的距離為 1('ad'),
從“a”到“e”的距離為 2('ab'-'be')或('ad'-'de'),
從“a”到“f”的距離為 2('ac'-'cf')或('ad'-'df'),
從“a”到“g”的距離為 3('ac'-'cf'-'fg')或('ad'-'df'-'fg')。
因此離心率為 3,這是從頂點“a”到距離最大的“ag”之間的最大值。
換句話說,
e(b) = 3
e(c) = 3
e(d) = 2
e(e) = 3
e(f) = 3
e(g) = 3
連通圖的半徑
所有頂點中最小離心率被認為是圖 G 的半徑。所有頂點到所有其他頂點的最大距離中的最小值被認為是圖 G 的半徑。
符號 - r(G)
在圖中所有頂點的離心率中,連通圖的半徑是所有這些離心率中的最小值。
例子
在上圖中,r(G) = 2,這是“d”的最小離心率。
圖的直徑
所有頂點中最大離心率被認為是圖 G 的直徑。所有頂點到所有其他頂點的距離中的最大值被認為是圖 G 的直徑。
**符號 - d(G)** - 在圖中所有頂點的離心率中,連通圖的直徑是所有這些離心率中的最大值。
例子
在上圖中,d(G) = 3;這是最大離心率。
中心點
如果圖的離心率等於其半徑,則稱為圖的中心點。如果
e(V) = r(V),
則“V”是圖“G”的中心點。
例子
在示例圖中,“d”是圖的中心點。
e(d) = r(d) = 2
中心
“G”的所有中心點的集合稱為圖的中心。
例子
在示例圖中,{'d'} 是圖的中心。
周長
**“G”的最長環中的邊數**稱為“G”的周長。
例子
在示例圖中,周長為 6,我們從最長環 a-c-f-g-e-b-a 或 a-c-f-d-e-b-a 中推匯出。
圈數
“G”的最短環中的邊數稱為其圈數。
**符號:**g(G)。
**示例** - 在示例圖中,圖的圈數為 4,我們從最短環 a-c-f-d-a 或 d-f-g-e-d 或 a-b-e-d-a 中推匯出。
頂點度數和定理
如果 G = (V, E) 是一個具有頂點 V = {V1, V2,…Vn} 的無向圖,則
推論 1
如果 G = (V, E) 是一個具有頂點 V = {V1, V2,…Vn} 的有向圖,則
推論 2
在任何無向圖中,具有奇數度的頂點數為偶數。
推論 3
在無向圖中,如果每個頂點的度數為 k,則
推論 4
在無向圖中,如果每個頂點的度數至少為 k,則
| 推論 5
在無向圖中,如果每個頂點的度數至多為 k,則