多邊形的外部角

---

引言

多邊形的外部角是由多邊形的一條邊及其另一條邊的延長線所形成的。多邊形是幾何學中一個基本且重要的形狀。多邊形是一個封閉的二維幾何圖形，具有三條或更多條邊。希臘語中的“多邊形”由兩個片語成：“poly”意為多，“gon”意為角。多邊形在現實生活中的一些例子包括六邊形的形狀，筆記型電腦的矩形螢幕，百慕大三角，埃及金字塔等等。三角形被廣泛應用於現代建築中。多邊形有兩種型別的角：外角和內角。內角是在多邊形內部形成的角，而外角是在多邊形外部形成的角。

多邊形

• 多邊形是一個封閉的二維幾何圖形，具有兩條或更多條邊。

• 如前所述，多邊形是封閉形狀，沒有開放的端點。

• 多邊形的邊長和角的大小可能相同也可能不同。

• 三角形、五邊形和六邊形是多邊形的一些例子。

• 多邊形根據邊長、角的大小和邊的數量進行分類。

根據邊數對多邊形的分類：

序號	多邊形名稱	邊數
1	三角形	3
2	四邊形	4
3	五邊形	5
4	六邊形	6
5	七邊形	7
6	八邊形	8
7	九邊形	9
8	十邊形	10
9	十一邊形	11
10	十二邊形	12

根據邊長和角的大小對多邊形的分類：

• 根據邊長，多邊形分為兩種型別

  • 正多邊形

  • 非正多邊形

正多邊形

• 如果多邊形的邊長和角相等，則該多邊形稱為正多邊形。

• 這些多邊形被稱為等角多邊形和等邊多邊形。

• 例如，正方形的所有邊和角都相等，因此正方形是正多邊形。

非正多邊形

• 如果多邊形的邊長和角不相等，則該多邊形稱為非正多邊形。

• 例如，不等邊三角形是非正多邊形的最佳例子，不等邊三角形的邊長和角不相等。

根據多邊形角的大小對多邊形的分類

• 根據角的大小，多邊形分為凸多邊形和凹多邊形兩種型別。

凸多邊形

• 如果內角的度數總是小於180⁰，則這些多邊形稱為凸多邊形。

• 凸多邊形的頂點總是指向外側。

• 例如，六邊形、五邊形和七邊形是凸多邊形的一些例子。

凹多邊形

• 凹多邊形與凸多邊形正好相反。

• 在凹多邊形中，一個角的度數大於180⁰。

• 凹多邊形的頂點總是指向內側和外側。

正多邊形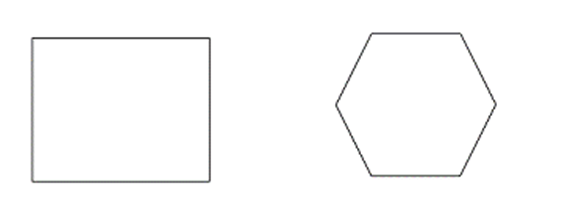
非正多邊形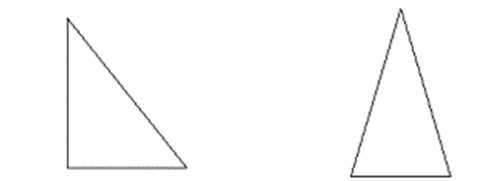
凸多邊形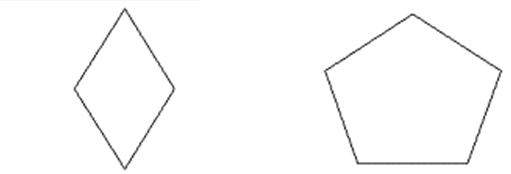
凹多邊形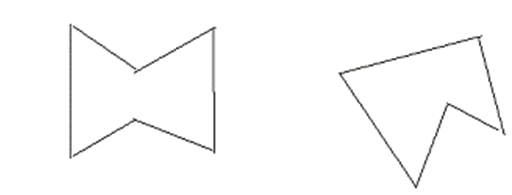

上圖顯示了不同型別的多邊形。

多邊形的角

• 如前所述，多邊形中有兩種型別的角，如下所示：

  • 內角

  • 外角

多邊形的內角

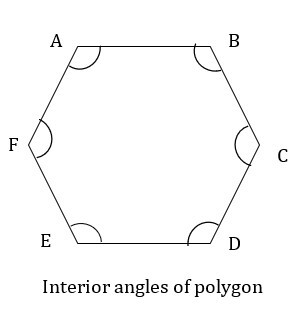
任何物體內部形成的角都稱為內角。多邊形的內角是在多邊形的兩條相鄰邊之間形成的角。內角的數量等於邊的數量。

計算內角的公式為：

$$\mathrm{內角 = 180^0×(n-2)}$$

其中n是多邊形的邊數。

內角度數 $\mathrm{=\frac{180^0-n}{n}}$

多邊形的外角

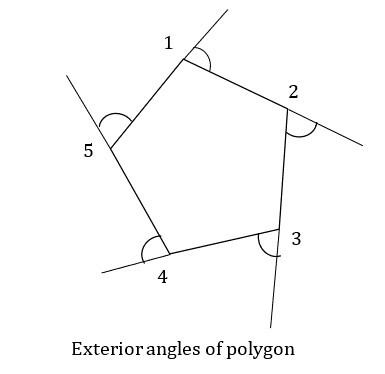
這些角是在多邊形外部形成的角。上圖顯示了這些角。延長多邊形的一條邊後，由相鄰邊和延長線所成的角稱為外角。

假設你從頂點$\mathrm{\angle 1}$開始，沿順時針方向移動，你經過$\mathrm{\angle 2, \angle 3, \angle 4\: \&\: \angle 5}$回到同一個頂點。一個完整的旋轉等於360⁰。因此，任何多邊形的外角之和為360⁰。

外角的度數可以透過將360⁰除以邊數來計算。公式為：

$$\mathrm{外角度數 = \frac{360^0}{n}}$$

多邊形外角定理

定理：對於凸多邊形，考慮每個外角，外角之和為360⁰。

證明：考慮一個有n條邊的多邊形。外角之和為N，對於任何封閉圖形，外角之和等於線性對和內角之和。

$$\mathrm{∴ N=180n-180(n-2)}$$

$$\mathrm{N=180n-180n+360}$$

$$\mathrm{N=360}$$

因此，多邊形外角之和為360⁰。

例題

1) 計算正五邊形的每個外角的度數。

解：外角 $\mathrm{=\frac{360}{n}}$

對於五邊形，n = 5

外角 = $\mathrm{\frac{360}{5}=72^0}$

因此，五邊形的每個外角的度數為72⁰。

2) 求一個正十八邊形的每個外角的度數。

解：這裡n= 18

外角 = $\mathrm{\frac{360}{n}=\frac{360}{18}=20^0}$

因此，十八邊形的每個外角的度數為20⁰。

3) 如果多邊形的內角之和為2160⁰，求多邊形的邊數？

解：多邊形的內角之和 = (n-2)×180⁰

$$\mathrm{2160^0 = (n-2)×180^0}$$

$$\mathrm{\frac{2160^0}{180^0}=(n-2)}$$

$$\mathrm{(n-2) = 12}$$

$$\mathrm{n = 14}$$

因此，多邊形的邊數為14。

結論

在本教程中，我們討論了多邊形、多邊形的角和多邊形的外角，並透過例題進行了講解。在幾何學中，多邊形是一個具有三條或三條以上邊的二維封閉形狀。多邊形根據邊長、角的大小和邊數進行分類。在一個多邊形中，可以找到兩種型別的角：內角和外角。我們還學習了計算多邊形內角和外角的公式。

常見問題

1. 什麼是遠內角？

與外角不相鄰且不共享外角頂點的角稱為遠內角。

2. 六邊形的角的度數是多少？

六邊形的每個內角和外角的度數分別為120⁰和60⁰。

3. 菱形可以是多邊形嗎？

是的。菱形是四邊形。四邊形是一種多邊形，因此所有菱形都是多邊形。

4. 所有多邊形的外角之和都等於360⁰嗎？

任何型別多邊形的外角之和都為360⁰。

5. 外角性質是什麼？

在三角形中，外角的度數等於兩個內角度數之和。