資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學資料結構中的尤拉圖和哈密頓圖
在本節中，我們將瞭解尤拉圖和哈密頓圖。但在深入探討之前，我們首先需要了解圖中的軌跡。假設我們有一個如下所示的圖：
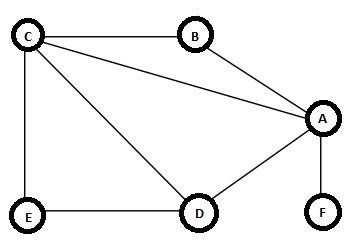
軌跡是一條路徑，它是一系列邊 (v1, v2), (v2, v3), …, (vk - 1, vk)，其中所有頂點 (v1, v2, … , vk) 可能不盡相同，但所有邊都不同。在這個例子中，一個軌跡是 {(B, A), (A, C), (C, D), (D, A), (A, F)}。這是一個軌跡。但它不被認為是簡單路徑，因為頂點 A 被訪問了兩次。如果第一個和最後一個頂點相同，則它將是一個閉合軌跡。
尤拉跡
在圖 G(V, E) 中，尤拉跡是指包含每條邊恰好一次的軌跡。如果 G 具有閉合尤拉跡，則該圖稱為尤拉圖。換句話說，我們可以說，如果從一個頂點開始，我們可以遍歷每條邊恰好一次並返回到起始頂點，則圖 G 將是尤拉圖。尤拉證明，當且僅當其每個頂點的度數均為偶數時，圖才稱為尤拉圖。
哈密頓迴路
如果一個迴路經過圖 G 的每個頂點，則該回路稱為哈密頓迴路。許多不同的定理給出了圖成為哈密頓圖的充分條件。然而，確定任意圖是否為哈密頓圖的問題是一個 NP 完全問題。
更新於：2020年8月10日
瀏覽量 1K+
廣告