尤拉路徑和哈密頓路徑

如果可以在不重複相同路徑的情況下，在所有頂點之間繪製一條路徑，則該圖是可遍歷的。基於此路徑，有一些類別，例如尤拉路徑和歐拉回路，在本節中進行了描述。

尤拉路徑

尤拉路徑包含圖“G”中的每條邊恰好一次，並且包含圖“G”中的每個頂點至少一次。如果連通圖 G 包含尤拉路徑，則稱該圖是可遍歷的。

示例

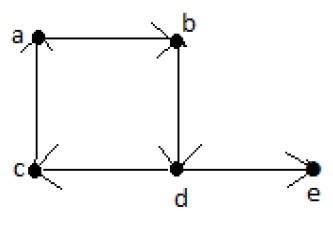
**尤拉路徑** = d-c-a-b-d-e。

歐拉回路

在尤拉路徑中，如果起始頂點與其結束頂點相同，則稱為歐拉回路。

示例

**尤拉路徑** = a-b-c-d-a-g-f-e-c-a。

歐拉回路定理

連通圖“G”是可遍歷的當且僅當 G 中具有奇數度的頂點數恰好為 2 或 0。如果一個連通圖 G 恰好有兩個具有奇數度的頂點，則它可以包含尤拉路徑，但不能包含歐拉回路。

**注意** - 此尤拉路徑以一個奇數度頂點開始，以另一個奇數度頂點結束。

示例

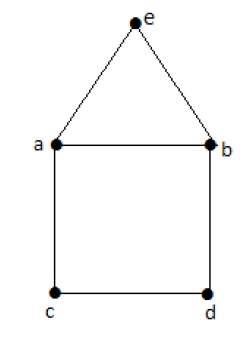
**尤拉路徑** - b-e-a-b-d-c-a 不是歐拉回路，但它是尤拉路徑。顯然，它恰好有兩個奇數度頂點。

**注意** - 在連通圖 G 中，如果具有奇數度的頂點數 = 0，則存在歐拉回路。

哈密頓路徑

如果一個連通圖包含圖 G 中的每個頂點恰好一次，則稱該圖是哈密頓圖。這樣的路徑稱為**哈密頓路徑**。

示例

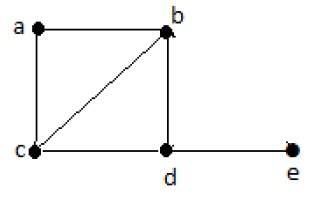
**哈密頓路徑** - e-d-b-a-c。

**注意** -

• 歐拉回路包含圖中每條邊恰好一次。
• 在哈密頓迴路中，可以跳過圖中的一些邊。

示例

請看下圖 -

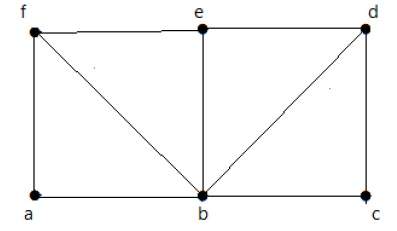
對於上面顯示的圖 -

• 存在尤拉路徑 – 錯誤
• 存在歐拉回路 – 錯誤
• 存在哈密頓迴路 – 正確
• 存在哈密頓路徑 – 正確

G 有四個奇數度頂點，因此它不可遍歷。透過跳過內部邊，該圖具有一個經過所有頂點的哈密頓迴路。

Mahesh Parahar

更新於: 2019-08-23

8K+ 瀏覽量

開啟你的 職業生涯

透過完成課程獲得認證

開始學習