哈密頓圖

哈密頓圖 - 如果存在一個環包含圖 G 的每個頂點並且該環稱為哈密頓環，那麼連通圖 G 被稱為哈密頓圖。圖 G 中的哈密頓路徑是恰好經過每個頂點一次的路徑。

狄拉克定理 - 如果 G 是一個具有 n 個頂點的簡單圖，其中 n ≥ 3 並且對於每個頂點 v，deg(v) ≥ {n}/{2}，那麼圖 G 是哈密頓圖。

奧爾定理 - 如果 G 是一個具有 n 個頂點的簡單圖，其中 n ≥ 2 並且對於每個不相鄰的頂點 x 和 y，deg(x) + deg(y) ≥ n，那麼圖 G 是哈密頓圖。

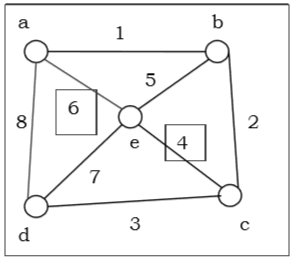
在上面的示例中，頂點 a 和 c 的度之和為 6，大於總頂點數 5，使用奧爾定理，它是一個哈密頓圖。

非哈密頓圖

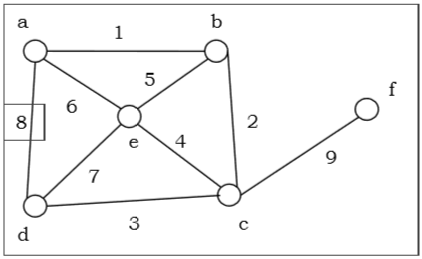
在上面的示例中，頂點 a 和 f 的度之和為 4，小於總頂點數 4，使用奧爾定理，它不是哈密頓圖。

Mahesh Parahar

更新時間： 2019 年 8 月 23 日

14K+ 瀏覽量

開啟你的 職業生涯

透過完成課程取得認證

立即開始