資料結構中的自適應合併排序

自適應合併排序

自適應合併排序執行的是已排序子列表的合併，就像合併排序一樣。但是，初始子列表的大小取決於列表元素之間是否存在順序，而不是具有大小為 1 的子列表。例如，考慮圖中的列表。

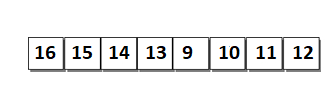
它包含 2 個已排序的子列表。

• 子列表 1 包含元素 16、15、14、13。
• 子列表 2 包含元素 9、10、11、12。

子列表 1 已排序，但順序相反。因此，子列表 1 反轉，如圖所示。

一旦找到子列表，合併過程就開始了。自適應合併排序開始合併子列表。自適應合併排序只需要一步合併，因為只有 2 個子列表。合併的結果如圖所示。

設計理念

• 首先找到已經按要求或反向排序的子列表
• 如果存在任何元素順序相反的子列表，則透過交換第一個元素和最後一個元素、第二個元素和倒數第二個元素等來反轉子列表。
• 繼續合併子列表以生成新的子列表，直到只剩下 1 個子列表。

自適應合併排序分析

自適應合併排序不是從大小為 1 的子列表開始，而是查詢已經按要求或反向排序的子列表。最初找到的子列表的大小至少為 2，最大為 m（m 為元素數量）。

但是，如果子列表包含反向順序的元素，則在開始合併操作之前會反轉列表。列表的反轉需要 (m/2) 次交換操作。

最佳情況

如果列表已經按順序或反向順序排序，則自適應合併排序將只有一個列表，並且不需要任何合併操作。但是，查詢列表是否已排序需要 O(m) 次比較操作，如果列表按反向順序排序，則需要 (m/2) 次交換操作。這使得自適應合併排序即使在列表按反向順序排序時也能適應。

因此，最佳情況下的時間複雜度計算如下：

T(m) = (m-1)+(m/2)
T(m) = (2m-2+m)/2
T(m) = O(m).

但是，與合併排序相比，自適應合併排序實現了 O(m) 的額外空間。

最壞情況

自適應合併排序將找到已按要求或反向排序的子列表。但是，在最壞情況下，沒有部分或完全排序的元素。因此，最初找到的子列表的大小將為 2。一旦找到子列表，合併過程就開始了。

• 大小為 2 的子列表的合併會產生大小為 4 的已排序子列表。
• 大小為 4 的子列表的合併會產生大小為 8 的已排序子列表。
• 合併過程持續進行，直到 2k < m。其中 k 是第 k 次合併步驟。

由於自適應合併排序的最壞情況下的合併步驟與合併排序相同。因此，自適應合併排序的最壞情況下的時間複雜度與合併排序類似：

T(m) = O(m log m).

Arnab Chakraborty

更新於: 2020年1月7日

675 次瀏覽

開啟您的 職業生涯

透過完成課程獲得認證

開始學習