圓錐

---

引言

圓錐底部有一個曲面；因此，它包含兩個表面積，總表面積是圓錐覆蓋的總表面積，而曲面面積由曲面覆蓋的表面積組成，即除底部圓形平面表面以外的表面積。圓錐有一個頂點或頂端和一條斜高。

在本教程中，我們將討論圓錐、斜高、曲面面積、總表面積以及一些已解決的示例。

圓錐

圓錐是三維圖形，底部有一個圓形平面作為底座，圓周上的線段連線到稱為頂點或頂端的點。它的形狀像金字塔，但具有圓形橫截面而不是三角形橫截面。

圓錐是一個三維立體幾何物體，頂部有一個尖頂，底部是一個圓形底座。圓錐有一個頂點和一個面。對於圓錐，沒有邊。

斜高

斜高定義為從頂點或頂端到圓錐圓形底座的距離。斜高的公式是從勾股定理推匯出來的，考慮由圓錐的半徑、高度和斜高形成的直角三角形。

下圖是一個圓錐，其中表示了圓錐的所有尺寸。

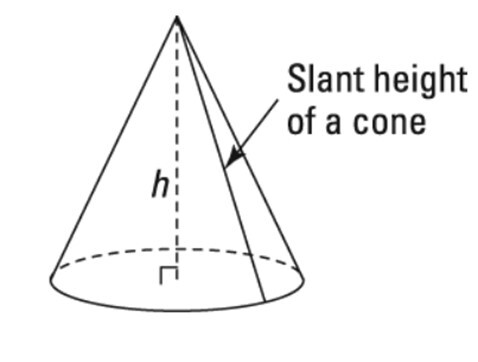
$\mathrm{圓錐的斜高(l)\:等於\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

圓錐的CSA（曲面面積）

曲面面積是在三維平面中由曲面（不包括圓形底座的表面）覆蓋的面積。簡而言之，稱為CSA。

• 曲面面積是不包括平面表面（即圓錐的圓形底座）的面積。

• 曲面面積的公式等於π乘以圓錐的半徑乘以圓錐的斜高。它以平方單位測量。

• $\mathrm{圓錐的CSA\:=\:\pi\:\times\:r\times\:l}$

我們知道$\mathrm{圓錐的斜高(l)\:等於\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

$$\mathrm{圓錐的CSA\:=\:\pi\:\times\:r\times\:\sqrt{h^{2}\:+\:r^{2}}}$$

圓錐的TSA（總表面積）

總表面積是在三維平面中由整個圓錐（曲面和平面）覆蓋的面積。簡而言之，稱為TSA。

• 它等於圓錐曲面面積與圓錐圓形底座面積的和。圓形底座的面積等於π乘以圓錐半徑的平方。

• 我們現在知道了圓錐的CSA，將π乘以圓錐半徑的平方加到CSA中以得到圓錐的TSA。它以平方單位測量。

• $\mathrm{圓錐的TSA\:=\:\pi\:\times\:r\times\:l\:+\:\pi\:\times\:r^{2}}$

$$\mathrm{圓錐的TSA\:=\:\pi\:\times\:r\times\:(l\:+\:r)}$$

我們知道$\mathrm{圓錐的斜高(l)\:等於\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

因此$\mathrm{圓錐的TSA\:=\:\pi\:\times\:r\times\:(\sqrt{h^{2}\:+\:r^{2}}\:+\:r)}$

圓錐的體積

圓錐佔據的空間量或容量稱為其體積。圓錐的底座是圓形的，因此它由半徑和直徑組成。然後你可以從底座的中心到圓錐的最頂端部分，這被測量為高度（當然，在冰淇淋的情況下，這個區域在底部）。

• 將圓錐底座的面積乘以圓錐的高度，再乘以三分之一，即可得到圓錐的體積。

• $\mathrm{圓錐的體積\:=\:\frac{1}{3}\pi\:r^{2}h}$

已解決的示例

1) 求半徑為2米，高為3米的圓錐的體積？

答案 - 給定半徑為2米，高為3米，我們知道立方體的體積為

$$\mathrm{圓錐的體積\:=\:\frac{1}{3}\pi\:r^{2}h}$$

$$\mathrm{圓錐的體積\:=\:\frac{1}{3}\pi\:2^{2}h}$$

$$\mathrm{圓錐的體積\:=4\pi}$$

2) 求半徑為2釐米，斜高為4釐米的圓錐的CSA？

答案 - 給定半徑為2釐米，斜高為4釐米，我們知道

$$\mathrm{圓錐的CSA\:=\:\pi\:\times\:r\times\:l}$$

$$\mathrm{=\:\pi\:\times\:2\times\:3}$$

$$\mathrm{圓錐的CSA\:=6\pi}$$

3) 如何根據面、邊和頂點定義圓錐？

答案 - 2個面，1條邊，1個頂點

其中一個面是圓形底座，另一個是連續的曲面。

唯一的一條邊是圓形底座的邊，兩個面在此處相遇。

頂點是頂部的點（尖角）。

4) 求半徑為2釐米，斜高為3釐米的圓錐的TSA？

答案 - 給定半徑為2釐米，斜高為3釐米

現在應用根據半徑和斜高計算圓錐TSA的公式，即

$$\mathrm{圓錐的TSA\:=\:\pi\:\times\:r\times\:l\:+\:\pi\:\times\:r^{2}}$$

$$\mathrm{=\:\pi\:\times\:2\times\:3\:+\:\pi\:\times\:2^{2}}$$

$$\mathrm{=\:10\pi}$$

因此，$\mathrm{圓錐的TSA\:=\:10\pi}$

5) 求高為5釐米，半徑為12釐米的圓錐的斜高？

答案 - 給定高為5釐米，半徑為12釐米，我們知道

$\mathrm{圓錐的斜高(l)\:等於\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

$$\mathrm{l\:=\:\sqrt{12^{2}\:+\:5^{2}}}$$

$$\mathrm{l\:=\:13}$$

因此$\mathrm{圓錐的斜高(l)\:等於\:l\:=\:13}$

結論

圓錐是一個包含圓形底座的3D圖形。它像金字塔；它包含圓形底座，而不是三角形底座。圓錐的表面積是圓錐覆蓋的表面。它有兩個表面積：曲面面積和總表面積。

常見問題

1. 圓錐是什麼意思？

圓錐是三維圖形，底部有一個圓形平面作為底座，圓周上的線段連線到稱為頂點或頂端的點。

2. 金字塔和圓錐有什麼區別？

兩者都是具有不同底座的3D圖形，金字塔具有三角形底座，而圓錐具有圓形底座

3. 圓錐的斜高是什麼意思？

斜高定義為從頂點或頂端到圓錐圓形底座邊界的距離。

4. 圓錐有哪些不同型別？

圓錐有兩種型別：

• 直圓錐

• 斜圓錐。

5. 斜圓錐是什麼意思？

圓錐具有圓形底座，並且頂點和底座的中心不在同一軸線上。頂點不在底座中心的上方。