從以下四個選項中選擇正確答案
菱形的兩條對角線的長度分別為 \( 16 \mathrm{~cm} \) 和 \( 12 \mathrm{~cm} \)。
(A) \( 9 \mathrm{~cm} \)
(B) \( 10 \mathrm{~cm} \)
(C) \( 8 \mathrm{~cm} \)
(D) \( 20 \mathrm{~cm} \)

已知

菱形的兩條對角線的長度分別為 \( 16 \mathrm{~cm} \) 和 \( 12 \mathrm{~cm} \)。

求解

我們需要求出菱形的邊長。

解答

我們知道，

菱形的對角線互相垂直平分。

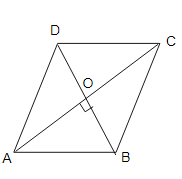
從圖中可以看出，

$AC=16\ cm$ 且 $BD=12\ cm$

$\angle AOB=90^o$

$AO=\frac{1}{2}AC$

$=\frac{1}{2}(16)\ cm$

$=8\ cm$

$BO=\frac{1}{2}BD$

$=\frac{1}{2}(12)\ cm$

$=6\ cm$

在直角三角形 AOB 中，根據勾股定理，

$AB^2=AO^2+OB^2$

$AB^2=8^2+6^2$

$=64+36$

$=100$

$AB=\sqrt{100}$

$=10\ cm$

菱形的邊長為 $10\ cm$。

教程點

更新於： 2022 年 10 月 10 日

51 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習