質心

---

引言

在數學中，質心指的是二維平面圖形的幾何中心。在本教程中，我們將學習質心以及三角形的其他中心及其之間的關係。

什麼是質心？

在數學中，質心指的是二維平面圖形的幾何中心。它是透過取平面圖形上所有點的算術平均值來確定其位置的點。“質心”一詞也指重心。

確定三角形的質心 - 三角形的三條中線相交的點稱為質心。三角形的中線是一條連線頂點與其對面中點的線段。

對於三角形 ABC，具有 AA₁、BB₁ 和 CC₁ 作為中線，用 p 表示的質心如下所示。

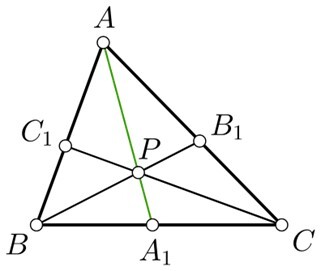
三角形的其他中心

除了質心之外，三角形還有三種類型的中心，即垂心、內心和外心。

• 垂心 - 從三角形的頂點垂直於其對邊作垂線，其交點稱為垂心。

  垂心可能位於三角形內部或外部，這取決於三角形的型別。

在上圖中，三條垂線的交點是垂心。

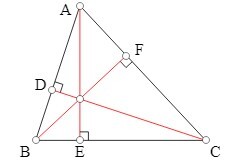
• 內心 - 三角形的三條內角平分線的交點構成三角形的內心。

  內接於三角形的三角形內切圓的圓心也稱為三角形的內心。

在上圖中，三條內角平分線的交點是內心，用 I 表示。

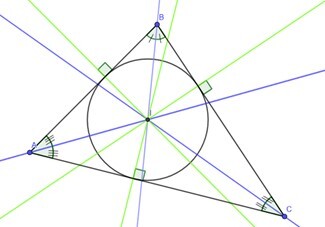
• 外心 - 三角形的外心可以作為三角形所有邊的垂直平分線的交點求出。

  三角形的每個頂點到外心的距離都相等。

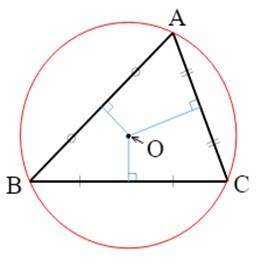
在上圖中，三條垂直平分線的交點是外心，用 O 表示。

質心的性質

• 質心是物體的幾何中心。

• 平面圖形中所有點的算術平均位置稱為圖形的質心或幾何中心。

• 三角形的質心始終位於三角形內，因為中線位於三角形內。

• 可以透過對三角形三條邊的 x 和 y 座標取平均值來確定質心。

• 質心是三角形中最常見的併發點。其在數學和物理學中的重要性源於它是三角形的幾何中心。

• 質心將中線分成 2:1 的比例。

  • 最長線段最靠近頂點，質心將每條中線分成長度為 2:1 的兩條線段。

• 質心定理：三角形的質心位於從頂點到邊的中點的距離的 2/3 處。

  • 對於三角形 ABC，具有 A¹、B¹ 和 C¹ 作為中線，質心 p

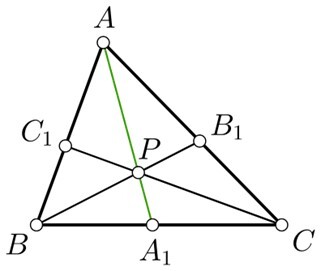
• 這裡使用質心定理，$\mathrm{AP=\frac{2}{3} AA_1}$

• 類似地，$\mathrm{BP=\frac{2}{3} BB_1\:and\: CP=\frac{2}{3} CC_1}$

三角形質心的座標

可以透過取三角形頂點的平均值來計算質心的座標。

對於三角形 ABC，具有 A¹、B¹ 和 C¹ 作為中線，並且設 A 頂點的座標為 (x¹,y¹)，B 頂點的座標為 (x²,y²)，C 頂點的座標為 (x³,y³)，則

質心的座標為 $C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}).$

質心座標的推導

在上圖三角形 ABC 中，設 A 頂點的座標為 (x¹,y¹)，A 頂點的座標為 (x²,y²)，C 頂點的座標為 (x³,y³)

這裡三角形的中點分別是 BC、AC 和 AB 的 A¹、B¹ 和 C¹，我們知道中線將三角形的邊分成兩等分。

現在透過應用中點公式對於 A¹，A¹ 的座標將是，$\mathrm{(\frac{x_2+x_3}{2},\frac{y_2+y_3}{2})}$

現在根據質心的性質，如上所述，質心將中線分成 2:1 的比例，因此我們可以使用截面公式。

設 P 為三角形 ABC 的質心，

$$\mathrm{P=(\frac{\frac{2(x_2+x_3)}{2}+1(x_1)}{2+1},\frac{\frac{2(y_2+y_3)}{2}+1(y_3)}{2+1})}$$

簡化後，

$$\mathrm{P=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$$

等邊三角形

等邊三角形是三條邊長度相等的三條邊。等邊三角形的質心位於三角形的中心。

從每個三角形頂點到對邊畫垂直線，以獲得質心。質心是所有這些垂直線（長度都相等）相交的地方。

等邊三角形的中線、角平分線和高線都相同。因此，等邊三角形的所有中心都相同。

可以計算質心到等邊三角形任何頂點的距離 -

設 a 為等邊三角形中任何一邊的長度，根據等邊三角形的性質，我們知道等邊三角形的高度為：

$$\mathrm{h=\frac{√3}{2} a}$$

根據質心的性質，我們知道質心將中線分成 2:1 的比例。

因此，等邊三角形質心到其任何頂點的距離

= 等邊三角形高度的 2/3 =$\mathrm{\frac{2}{3}×\frac{√3}{2} a}$

$$\mathrm{=\frac{a}{√3}.}$$

例題

1) 求座標為 P(15,4)、Q(4,-6)、R(5,12) 的三角形的質心

求質心座標的公式為，$\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$

因此，這裡我們有 x_1=15，x_2=4，x_3=5 和 y_1=4，y_2=-6，y_3=12

將這些值代入上述 C 的公式，我們有

$$\mathrm{C=(\frac{15+4+5}{3},\frac{4-6+12}{3})=(\frac{24}{3},\frac{10}{3})}$$

因此，質心的座標為，$\mathrm{(8,\frac{10}{3})}$.

2) 求座標為 A(-3,3)、B(3,1)、C(-1,-1) 的三角形的質心

求質心座標的公式為，$\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$

因此，這裡我們有 x₁=-3，x₂=3，x₃=-1 和 y₁=3，y₂=1，y₃=-1

將這些值代入上述 C 的公式，我們有

$$\mathrm{C=(\frac{-3+3-1}{3},\frac{3+1-1}{3})=(\frac{-1}{3},\frac{3}{3})}$$

因此，質心的座標為，$\mathrm{(\frac{-1}{3},1).}$

結論

在數學中，質心指的是二維平面圖形的幾何中心。三角形的三個中線相交產生三角形的質心。它是三角形的四個併發點之一。角平分線的交點位於內心。而中線的交點稱為質心。雖然質心將其中線分成 2:1 的比例，但內心並不特別劃分角平分線。內心和質心都位於三角形內部。

常見問題

1. 什麼是三角形的質心？

三角形的三個中線相交產生三角形的質心。它是三角形的四個併發點之一。質心實際上是三角形的幾何中心。

2. 什麼是質心定理？

質心定理指出，三角形的質心位於從頂點到邊的中點的距離的 2/3 處。

3. 質心和內心有什麼區別？

角平分線的交點位於內心。而中線的交點稱為質心。雖然質心將其中線分成 2:1 的比例，但內心並不特別劃分角平分線。內心和質心都位於三角形內部。

4. 質心和垂心有什麼區別？

垂線的交點位於垂心。而中線的交點稱為質心，雖然質心將其中線分成 2:1 的比例，但垂心並不特別劃分角平分線。垂心位於三角形外部，而質心位於三角形內部。

5. 計算質心的公式是什麼？

可以透過取三角形頂點的平均值來計算質心的座標。對於三角形 ABC，設 A 頂點的座標為 (x₁,y₁)，B 頂點的座標為 (x₂,y₂)，C 頂點的座標為 (x₃,y₃)，則質心的座標為

$$\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}).}$$