重心與形心之間的區別

---

介紹

形心是指應用於幾何平衡圖形或物體的術語。它是該圖形或物體的中心。尋找對稱實體中心的 方法各不相同，但它確實存在，而且對此沒有疑問。

例如，三角形具有形心，它是三條中線的交點。與形心相反，重心是一個更廣泛的術語，涵蓋對稱 和非對稱物體和圖形。值得注意的是，對於對稱物體以及體積圖形和形狀，重心和形心是相同的。對於非對 稱物體，我們需要進行重量距離分析，並透過將其除以總重量來找到平均值，以找到重心的距離。下圖給 出了我們如何感知這兩個概念的想法

圖：1 不規則石頭的重心和梯形的形心

重心和形心對於二維圖形和體積圖形往往是相同的，並且由於它提供的穩定性和平衡性而很重要。在上 圖中，由於排列石頭時出現的傾斜以及石頭的不規則形狀，不規則石頭的重心將向左移動。在梯形的情況 下，一旦您有了 a、b 和 h，圖中就會給出公式。本文闡明瞭重心和形心的概念。它們在體積或質量物體的 中心或穩定性方面都是非常密切相關的術語，但在某些情況下卻有所不同。

重心 (COG)

重心是物體中一個假想的點，透過該點，地球的重力作用於物體的物質質量以產生其重量。在這一點 上，整個重量都集中起來，為該物體提供所需的穩定性。

這裡值得一提的是公式重量 = 質量 $\mathrm{\times}$ 重力；W = mg。重心是從物體上的參考點算起的距離。因此，其測量單位為米。

如果您以汽車的穩定性為例，就會很好地理解重心的重要性。汽車、卡車和車輛都有一個非常嚴格的設 計階段，在該階段，製造商會測試車輛的重心儘可能低，同時滿足所有其他要求。重心越低，車輛在道路 上的穩定性越好。

重心公式

參考下圖，該杆的兩端有兩個重量 - W1(5kg) 作用於 A 點，W2(2kg) 作用於 B 點。透過這種重量分佈，重 心作用於 G 點。

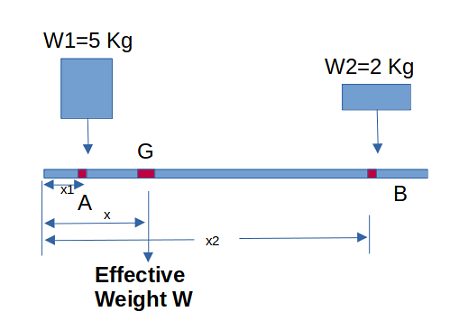
圖：2 尋找重心

在圖中標出了 x1 和 x2 距離，距離 x（COG）的方程式將為

$$\mathrm{x=\frac{(x_{1}W_{1}+x_{2}W_{2})}{(W_{1}+W_{2})}}$$

重心 (COG) 和質心 (COM) 之間的關係

重心是物體中一個假想的點，由於地球重力的影響，物體的重量在此點向下作用。質心是物體物質 中的一個點，在此點，作用在物體上的外力會使其沿外力預期方向移動。

除了預期的方向之外，沒有其他因素與被識別為質心的點相關聯。在許多情況下，這兩者會收斂到同一點。 但這兩者並不總是相同的。COG 由於重力而向下作用，而相反，COM 沿外力的預期方向作用。

練習題

Q1. 求長度為 10m 的直線的形心？

答：線的形心為

$$\mathrm{\frac{L}{2}=\frac{10}{2}=5\:米}$$

Q2. 求面積為 A 的圓的形心？

答：圓的形心是半徑 r。

$$\mathrm{A=\pi r^{2};所以\:r=\sqrt{\frac{A}{\pi }}}$$

Q3. 求長為 a、寬為 b 的矩形的形心？

答：矩形的形心的 X 座標為 $\mathrm{a/2}$，Y 座標為 $\mathrm{b/2}$

由於幾何圖形的形心或重心基於幾何原理，因此請參考所有可能圖形的公式以及良好的參考。

什麼是形心？

形心是指考慮沒有質量的幾何圖形（如圓形、三角形、正方形、梯形等）時的術語。當考慮有質量和重 量的物體時，使用重心一詞。

重心與形心的區別

序號	特徵	重心	形心
1	力的方向	垂直向下	沿外力的方向
2	主要標準	重量	幾何中心
3	表示為	點 G	點 C
4	計算/測量	透過物理特性	通過幾何方法
5	密度	允許物體內部密度變化	幾何圖案或圖形的密度均勻
6	演示	可以使用對稱或非對稱質量/密度分佈的物理物質進行演示	可以使用幾何概念和相同的驗證進行演示。

結論

本文詳細介紹了兩個有趣的概念。這兩個概念的共同點是對稱和平衡音調。這些主題分別從定義、核心 概念、方程式、與質心的關係、練習題以及最後但並非最不重要的兩個差異（形心和重心）方面進行了探 索。值得注意的是，在大多數情況下，這兩個概念是相同的，例如體積形狀和圖形；它們是相同的，可以 相互切換。對於具有質量的非對稱材料，兩者是不同的。對於具有質量的對稱材料，它們也可以相互切換， 因為它們收斂到物體物質中的同一點。

常見問題

Q1. 如何找到球體的形心？

答：如果您在 x-y-z 座標平面中考慮一個球體，並且如果其中心位於原點，則該球體的形心就是原點本身。如 果您是從球體的表面取的，則它距表面的任何一點的距離為 r（半徑）。

Q2. 重心的單位是什麼？

答：它是距離，因此單位為米。

Q3. 重心在運營中的含義是什麼？

答：重心是指在多箇中心中針對特定操作的最低運營成本中心。

Q4. 將電池連線到底盤的電動汽車能否為汽車提供更好的穩定性？

答：是的，這是一個受歡迎的副作用。根據設計，電池最好放置在地板上以進行保護和節省空間。這降低 了車輛的重心，從而減少了車輛的翻滾和事故，這是一個額外的好處。

Q5. 什麼是質量矩？

答：質量矩是質量與其到某一點的距離的乘積。