人工智慧 - 常用搜索演算法

搜尋是人工智慧中解決問題的通用技術。有一些單人遊戲，例如拼圖遊戲、數獨、填字遊戲等。搜尋演算法可以幫助你在這些遊戲中搜索特定位置。

單智慧體尋路問題

像 3X3 八塊拼圖、4X4 十五塊拼圖和 5X5 二十四塊拼圖這樣的遊戲都是單智慧體尋路挑戰。它們由帶有空白塊的矩陣組成。玩家需要透過垂直或水平地將棋子滑入空白格來排列棋子，以達到某個目標。

單智慧體尋路問題的其他例子包括旅行商問題、魔方和定理證明。

搜尋術語

問題空間 - 搜尋發生的場所。(一組狀態和一組改變這些狀態的運算子)
問題例項 - 初始狀態 + 目標狀態。
問題空間圖 - 表示問題狀態。狀態由節點表示，運算子由邊表示。
問題的深度 - 從初始狀態到目標狀態的最短路徑或最短操作序列的長度。
空間複雜度 - 儲存在記憶體中的最大節點數。
時間複雜度 - 建立的最大節點數。
可採納性 - 演算法始終找到最優解的屬性。
分支因子 - 問題空間圖中子節點的平均數量。
深度 - 從初始狀態到目標狀態的最短路徑長度。

暴力搜尋策略

它們是最簡單的，因為它們不需要任何特定領域的知識。它們在可能狀態數量較少的情況下效果很好。

要求：

狀態描述
一組有效的運算子
初始狀態
目標狀態描述

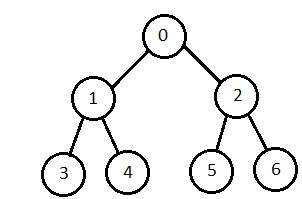
廣度優先搜尋

它從根節點開始，首先探索相鄰節點，然後移動到下一層鄰居。它一次生成一棵樹，直到找到解決方案。它可以使用 FIFO 佇列資料結構實現。這種方法提供了到解決方案的最短路徑。

如果分支因子（給定節點的子節點平均數量）= b，深度 = d，則 d 層的節點數 = b^d。

最壞情況下建立的節點總數為 b + b² + b³ + … + b^d。

缺點 - 由於每一層節點都儲存下來以建立下一層節點，因此它會消耗大量記憶體空間。儲存節點的空間需求呈指數級增長。

其複雜度取決於節點數。它可以檢查重複節點。

深度優先搜尋

它使用 LIFO 棧資料結構以遞迴方式實現。它建立與廣度優先方法相同的節點集，只是順序不同。

由於在每次迭代中從根節點到葉節點儲存單路徑上的節點，因此儲存節點的空間需求是線性的。分支因子為 *b*，深度為 *m*，則儲存空間為 *bm*。

缺點 - 此演算法可能不會終止，並且會在一條路徑上無限進行。解決這個問題的方法是選擇一個截止深度。如果理想截止值為 *d*，而選擇的截止值小於 *d*，則此演算法可能會失敗。如果選擇的截止值大於 *d*，則執行時間會增加。

其複雜度取決於路徑數。它不能檢查重複節點。

雙向搜尋

它從初始狀態向前搜尋，從目標狀態向後搜尋，直到兩者相遇以識別公共狀態。

初始狀態的路徑與目標狀態的反向路徑連線。每次搜尋僅進行到總路徑的一半。

一致代價搜尋

對到節點的路徑成本按遞增順序進行排序。它總是擴充套件成本最低的節點。如果每個轉換的成本相同，則它與廣度優先搜尋相同。

它按成本遞增的順序探索路徑。

缺點 - 可能存在多個成本 ≤ C* 的長路徑。一致代價搜尋必須全部探索它們。

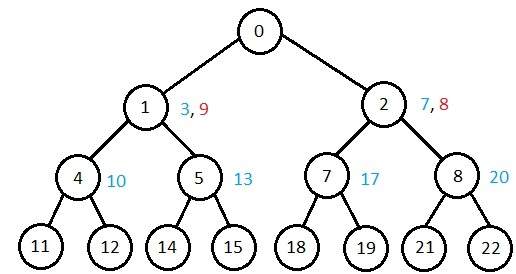
迭代加深深度優先搜尋

它對第 1 層執行深度優先搜尋，重新開始，對第 2 層執行完整的深度優先搜尋，並以此類推，直到找到解決方案。

它只有在生成所有較低節點後才會建立節點。它只儲存節點的堆疊。當它在深度 *d* 找到解決方案時，演算法結束。在深度 *d* 建立的節點數為 b^d，在深度 *d-1* 為 b^d-1。

各種演算法複雜度的比較

讓我們根據各種標準檢視演算法的效能：

標準	廣度優先	深度優先	雙向	一致代價	迭代加深
時間	b^d	b^m	b^d/2	b^d	b^d
空間	b^d	b^m	b^d/2	b^d	b^d
最優性	是	否	是	是	是
完整性	是	否	是	是	是

啟發式 (啟發) 搜尋策略

為了解決具有大量可能狀態的大型問題，需要新增特定於問題的知識以提高搜尋演算法的效率。

啟發式評估函式

它們計算兩個狀態之間最優路徑的成本。滑動塊遊戲的啟發式函式是透過計算每個塊與其目標狀態的移動次數並將所有塊的這些移動次數相加來計算的。

純啟發式搜尋

它按照啟發式值的順序擴充套件節點。它建立兩個列表，一個用於已擴充套件節點的封閉列表和一個用於已建立但未擴充套件節點的開放列表。

在每次迭代中，擴充套件具有最小啟發式值的節點，建立其所有子節點並將其放入封閉列表中。然後，將啟發式函式應用於子節點，並根據其啟發式值將其放入開放列表中。儲存較短的路徑，丟棄較長的路徑。

A* 搜尋

這是最著名的最佳優先搜尋形式。它避免擴充套件已經很昂貴的路徑，而是首先擴充套件最有希望的路徑。

f(n) = g(n) + h(n)，其中

g(n) 到達該節點的成本（迄今為止）
h(n) 從該節點到達目標的估計成本
f(n) 透過 n 到達目標的路徑的估計總成本。它使用優先順序佇列按 f(n) 遞增實現。

貪婪最佳優先搜尋

它擴充套件估計最接近目標的節點。它基於 f(n) = h(n) 擴充套件節點。它使用優先順序佇列實現。

缺點 - 它可能陷入迴圈。它不是最優的。

區域性搜尋演算法

它們從一個潛在的解決方案開始，然後移動到一個相鄰的解決方案。即使在它們結束之前任何時候中斷，它們也可以返回一個有效的解決方案。

爬山搜尋

這是一個迭代演算法，它從問題的任意解開始，並嘗試透過增量地更改解的單個元素來找到更好的解。如果更改產生了更好的解，則增量更改將作為新的解。重複此過程，直到沒有進一步的改進。

函式爬山(問題)，返回區域性最大值的狀態。

inputs: problem, a problem
local variables: current, a node
                 neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
   do neighbor <- a highest_valued successor of current
      if Value[neighbor] ≤ Value[current] then
      return State[current]
      current <- neighbor				  
	
end

缺點 - 此演算法既不完整也不最優。

區域性束搜尋

在此演算法中，它在任何給定時間都保留 k 個狀態。在開始時，這些狀態是隨機生成的。這些 k 個狀態的後繼者是藉助目標函式計算的。如果這些後繼者中的任何一個是目標函式的最大值，則演算法停止。

否則，將（初始 k 個狀態和狀態的 k 個後繼者 = 2k）個狀態放入池中。然後對池進行數值排序。選擇最高的 k 個狀態作為新的初始狀態。重複此過程，直到達到最大值。

函式束搜尋( *問題，k*)，返回一個解狀態。

start with k randomly generated states
loop
   generate all successors of all k states
   if any of the states = solution, then return the state
   else select the k best successors
end

模擬退火

退火是加熱和冷卻金屬以改變其內部結構以修改其物理性質的過程。當金屬冷卻時，其新結構被固定，金屬保持其新獲得的性質。在模擬退火過程中，溫度保持可變。

我們最初將溫度設定得很高，然後隨著演算法的進行緩慢“冷卻”。當溫度很高時，允許演算法以高頻率接受較差的解。

開始

初始化 k = 0；L = 整數變數數；
從 i → j，搜尋效能差異 Δ。
如果 Δ <= 0 則接受；否則，如果 exp(-Δ/T(k)) > random(0,1) 則接受；
對步驟 1 和 2 重複 L(k) 步。
k = k + 1；

重複步驟 1 到 4，直到滿足條件。

結束

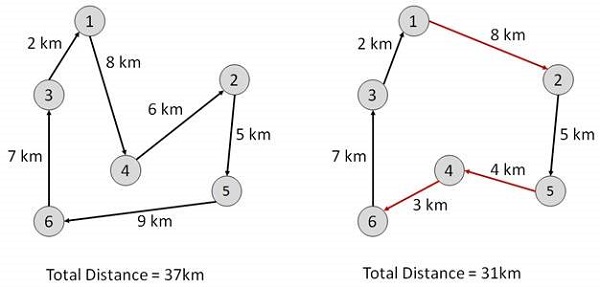
旅行商問題

在此演算法中，目標是找到一個低成本的路線，從一個城市開始，沿途精確訪問所有城市，並在同一起始城市結束。

Start
   Find out all (n -1)! Possible solutions, where n is the total number of cities.
   Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
   Finally, keep the one with the minimum cost.
end

列印頁面