
人工智慧 - 模糊邏輯系統
模糊邏輯系統 (FLS) 對不完整、模糊、失真或不準確(模糊)的輸入做出可接受但明確的輸出。
什麼是模糊邏輯?
模糊邏輯 (FL) 是一種推理方法,類似於人類的推理。FL 的方法模仿人類決策的方式,包括“是”和“否”數字值之間的所有中間可能性。
計算機可以理解的常規邏輯塊接受精確的輸入併產生明確的輸出,即 TRUE 或 FALSE,這相當於人類的“是”或“否”。
模糊邏輯的發明者 Lotfi Zadeh 觀察到,與計算機不同,人類的決策包括“是”和“否”之間的一系列可能性,例如:
| 當然是的 |
| 可能是的 |
| 無法說 |
| 可能不是 |
| 當然不是 |
模糊邏輯基於輸入的可能性級別來實現明確的輸出。
實施
它可以應用於各種規模和功能的系統,從小型微控制器到大型的基於網路的工作站控制系統。
它可以以硬體、軟體或兩者的結合方式實現。
為什麼使用模糊邏輯?
模糊邏輯對商業和實踐用途很有用。
- 它可以控制機器和消費產品。
- 它可能不會給出準確的推理,但會給出可接受的推理。
- 模糊邏輯有助於處理工程中的不確定性。
模糊邏輯系統架構
它有四個主要部分,如下所示:
模糊化模組 - 它將系統的輸入(即清晰的數字)轉換為模糊集。它將輸入訊號分成五個步驟,例如:
| LP | x 為大正 |
| MP | x 為中正 |
| S | x 為小 |
| MN | x 為中負 |
| LN | x 為大負 |
知識庫 - 它儲存專家提供的 IF-THEN 規則。
推理引擎 - 透過對輸入和 IF-THEN 規則進行模糊推理,模擬人類推理過程。
反模糊化模組 - 它將推理引擎獲得的模糊集轉換為清晰的值。

隸屬函式作用於變數的模糊集。
隸屬函式
隸屬函式允許您量化語言術語並以圖形方式表示模糊集。模糊集 A在論域 X 上的隸屬函式定義為 μA:X → [0,1]。
這裡,X的每個元素都對映到 0 到 1 之間的值。它被稱為隸屬度或隸屬程度。它量化了X中元素對模糊集A的隸屬程度。
- x 軸表示論域。
- y 軸表示 [0, 1] 區間內的隸屬度。
可以有多個隸屬函式適用於將數值模糊化。使用簡單的隸屬函式,因為使用複雜的函式不會提高輸出的精度。
LP、MP、S、MN 和LN 的所有隸屬函式如下所示:
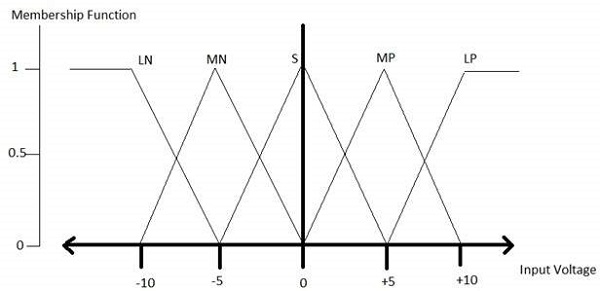
在各種其他隸屬函式形狀(如梯形、單點和高斯)中,三角形隸屬函式形狀最常見。
這裡,輸入到 5 級模糊器的範圍為 -10 伏到 +10 伏。因此,相應的輸出也會發生變化。
模糊邏輯系統示例
讓我們考慮一個帶有 5 級模糊邏輯系統的空調系統。該系統透過比較室溫與目標溫度值來調節空調的溫度。

演算法
- 定義語言變數和術語(開始)
- 為它們構建隸屬函式。(開始)
- 構建規則的知識庫(開始)
- 使用隸屬函式將清晰資料轉換為模糊資料集。(模糊化)
- 評估規則庫中的規則。(推理引擎)
- 組合每個規則的結果。(推理引擎)
- 將輸出資料轉換為非模糊值。(反模糊化)
發展
步驟 1 - 定義語言變數和術語
語言變數是以簡單單詞或句子的形式表示的輸入和輸出變數。對於室溫,冷、暖、熱等是語言術語。
溫度 (t) = {非常冷、冷、暖、非常暖、熱}
此集合的每個成員都是一個語言術語,它可以覆蓋整體溫度值的一部分。
步驟 2 - 為它們構建隸屬函式
溫度變數的隸屬函式如下所示:
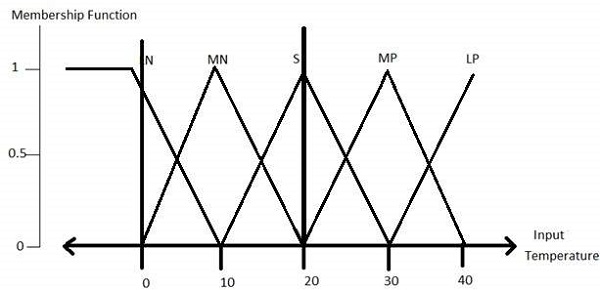
步驟 3 - 構建知識庫規則
建立一個室溫值與空調系統預期提供的目標溫度值的矩陣。
| 室溫/目標 | 非常冷 | 冷 | 暖 | 熱 | 非常熱 |
|---|---|---|---|---|---|
| 非常冷 | 無變化 | 加熱 | 加熱 | 加熱 | 加熱 |
| 冷 | 冷卻 | 無變化 | 加熱 | 加熱 | 加熱 |
| 暖 | 冷卻 | 冷卻 | 無變化 | 加熱 | 加熱 |
| 熱 | 冷卻 | 冷卻 | 冷卻 | 無變化 | 加熱 |
| 非常熱 | 冷卻 | 冷卻 | 冷卻 | 冷卻 | 無變化 |
將一組規則以 IF-THEN-ELSE 結構的形式構建到知識庫中。
| 序號 | 條件 | 行動 |
|---|---|---|
| 1 | 如果溫度 =(冷或非常冷)且目標 = 暖則 | 加熱 |
| 2 | 如果溫度 =(熱或非常熱)且目標 = 暖則 | 冷卻 |
| 3 | 如果(溫度 = 暖)且(目標 = 暖)則 | 無變化 |
步驟 4 - 獲取模糊值
模糊集運算執行規則評估。用於 OR 和 AND 的運算分別是 Max 和 Min。組合所有評估結果以形成最終結果。此結果是一個模糊值。
步驟 5 - 執行反模糊化
然後根據輸出變數的隸屬函式執行反模糊化。
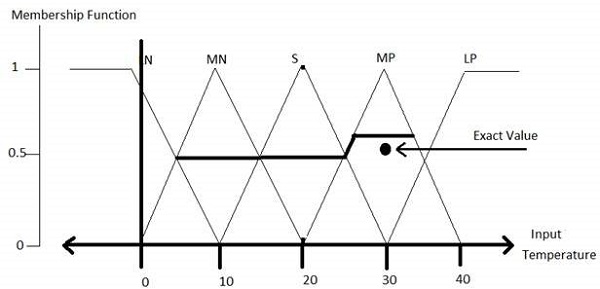
模糊邏輯的應用領域
模糊邏輯的關鍵應用領域如下所示:
汽車系統
- 自動變速箱
- 四輪轉向
- 車輛環境控制
消費電子產品
- 高保真音響系統
- 影印機
- 靜止和攝像機
- 電視
家用產品
- 微波爐
- 冰箱
- 烤麵包機
- 吸塵器
- 洗衣機
環境控制
- 空調/乾燥機/加熱器
- 加溼器
FLSs 的優點
模糊推理中的數學概念非常簡單。
由於模糊邏輯的靈活性,您可以透過新增或刪除規則來修改 FLS。
模糊邏輯系統可以接收不精確、失真、嘈雜的輸入資訊。
FLSs 易於構建和理解。
模糊邏輯是解決生活各個領域(包括醫學)中複雜問題的解決方案,因為它類似於人類的推理和決策。
FLSs 的缺點
- 模糊系統設計沒有系統的方法。
- 它們只有在簡單時才容易理解。
- 它們適用於不需要高精度的問 題。