面積

---

介紹

面積是指圖形所佔的空間。多邊形是由線段構成的平面封閉圖形的二維形狀。根據邊的數量，每個多邊形的名稱各不相同，例如三角形、四邊形等。圓和橢圓是封閉的二維形狀，沒有邊。面積是一個二維度量，表示二維形狀所覆蓋的空間量。

面積

面積是二維形狀內的空間。要測量多邊形的面積，當圖形在網格中時，我們可以使用單位正方形。透過計算網格中單位正方形的總數，我們可以計算該形狀的面積。當二維圖形不在網格中時，我們需要知道它們的長度和寬度才能找到它的面積。要找到圓的面積，將其分成扇形。

二維形狀的面積

對於封閉的二維形狀，我們可以使用方形網格來求面積。當二維圖形不在網格中並且已知邊、長或寬時，我們可以求出面積。

三角形的面積

三角形根據角度分為3種類型，根據邊分為3種類型。各種三角形的公式在表中給出。

型別	影像	公式
直角三角形		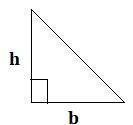$$\mathrm{面積 =\frac{1}{2}(底 × 高)}$$
等邊三角形或等角三角形		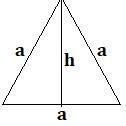$$\mathrm{面積 = \frac{\sqrt{3}}{4} a^2\: 或\: 0.433 \: a^2}$$ 其中 a = 邊長
等腰三角形		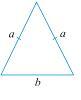$$\mathrm{面積 =\frac{1}{2}(底 × 高)}$$
不等邊三角形、鈍角三角形和銳角三角形		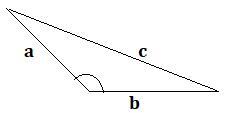$$\mathrm{面積 = \sqrt{s(s-a)(s-b)(s-c)}}$$ 其中 $\mathrm{s =\frac{a+b+c}{2}}$

四邊形的面積

型別	影像	公式
正方形		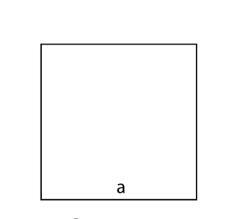面積 = a2 其中 a = 邊長
矩形		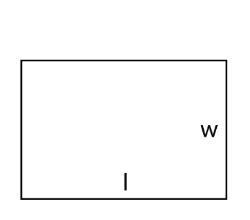面積 = 長 × 寬
平行四邊形		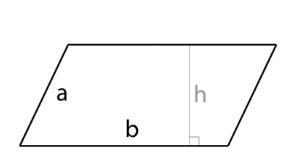面積 = 底 × 高
菱形		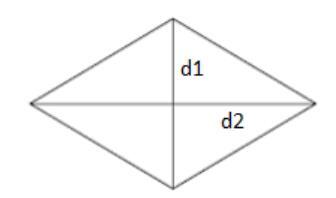面積 =$\mathrm{\frac{1}{2}(d_1×d_2)}$ 其中 d1 & d2 為對角線
梯形		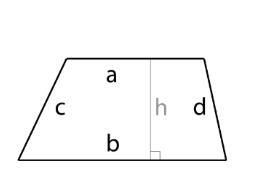$\mathrm{面積 =\frac{1}{2} (a+b)h}$ 其中 a $\&$ b 為平行邊，h 為高
四邊形		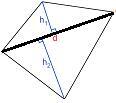$$\mathrm{面積 =\frac{1}{2} d(h_1+h_2)}$$ 其中 d = 對角線

多邊形的面積

• 多邊形可以有任意數量大於三條的邊。

• 要找到多邊形的面積，可以將多邊形分成若干個三角形和四邊形。

• 找到每個形狀的面積，然後加起來得到多邊形的面積。

圓和橢圓的面積

要找到圓的面積，我們需要將圓分成相等的部分，每個部分測量相等的度數，稱為扇形。現在我們可以排列每個扇形來形成一個矩形。我們知道，

$$\mathrm{圓的面積 = 矩形的面積 = l × b}$$

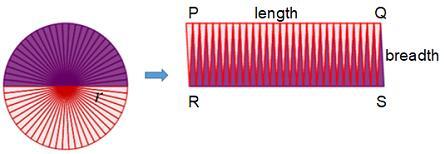
長度 PQ 覆蓋圓周的一半

$$\mathrm{其中\: PQ =\frac{1}{2} 圓的周長}$$

寬度 QS 覆蓋圓的半徑。

$$\mathrm{圓的面積 = \frac{1}{2}周長 × 半徑。}$$

我們知道圓的周長 = 2πr

$$\mathrm{圓的面積 = \frac{1}{2}(2πr) × r = πr^2}$$

現在要找到橢圓的面積，

橢圓是透過拉伸和收縮圓的半徑形成的。

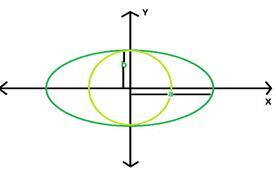
$$\mathrm{圓的面積 = 橢圓的面積}$$

$$\mathrm{π ×r×r = π×a×b}$$

其中 a 是長半軸的長度，b 是短半軸的長度。

例題

1)當底邊 = 4釐米，高 = 5釐米時，求三角形的面積。

答案

$$\mathrm{面積 =\frac{1}{2}(底 × 高)}$$

$$\mathrm{面積 = \frac{1}{2}(4 × 5) = \frac{1}{2}(20)}$$

$$\mathrm{面積 = 10 cm^2}$$

2)當 a = 2釐米時，求等邊三角形的面積。

答案

$$\mathrm{面積 = \frac{√3}{4} a^2}$$

$$\mathrm{面積 = \frac{√3}{4} 2^2}$$

$$\mathrm{= √3\: 或\: 1.732cm^2}$$

3) 當 a = 3釐米，b = 6釐米，c = 7釐米時，求三角形的面積。

答案

當三角形的每條邊長度不同時，我們可以應用海倫公式，首先求半周長，

$$\mathrm{s =\frac{a+b+c}{2} =\frac{3+6+7}{2} = \frac{16}{2} = 8 }$$

現在要找到三角形的面積，我們得到：

$$\mathrm{面積 = \sqrt{s(s-a)(s-b)(s-c)}}$$

$$\mathrm{面積 = \sqrt{8(8-3)(8-6)(8-7)}}$$

$$\mathrm{=\sqrt{80}}$$

4)當底邊 = 12釐米，高 = 11釐米時，求平行四邊形的面積。

答案

$$\mathrm{面積 = 底 × 高}$$

$$\mathrm{面積 = 12 ×11 = 121 cm^2}$$

5)菱形的周長為 20。如果一條對角線的長度為 8，則菱形的面積是多少？

答案

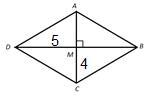
周長是菱形四條邊的總和，

$$\mathrm{20 = 4 s}$$

$$\mathrm{s = \frac{20}{4} = 5}$$

要根據已知值找到另一條對角線，我們可以將菱形分成 4 個三角形。

$$\mathrm{a = \frac{1}{2} (對角線) = \frac{1}{2} (8) = 4}$$

其中一個三角形有兩條已知邊，使用勾股定理，我們有：

$$\mathrm{ c^2 = a^2+ b^2}$$

$$\mathrm{5^2 = 4^2+ b^2}$$

$$\mathrm{ b = 3 }$$

因此對角線 d₂ = 3 × 2 = 6 和 d₂ = 8

現在求菱形的面積，

$$\mathrm{面積 =\frac{1}{2}(d_1×d_2)}$$

$$\mathrm{面積 =\frac{1}{2}(8×6)}$$

$$\mathrm{= 24cm^2}$$

6)求已知四邊形 ABCD 的面積

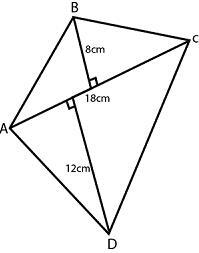
答案：已知，d = 18釐米，h₁ = 8釐米，h₂= 12釐米

$$\mathrm{面積 = \frac{1}{2} d(h_1+h_2)}$$

$$\mathrm{=\frac{1}{2} 18(8+12)}$$

$$\mathrm{= 180 cm^2}$$

7)如果橢圓的長軸 = 10釐米，短軸 = 6釐米，求橢圓的面積。

答案

$$\mathrm{a =\frac{1}{2}(10) = 5cm}$$

$$\mathrm{b =\frac{1}{2}(6) = 3cm }$$

$$\mathrm{橢圓的面積 = π×a×b}$$

$$\mathrm{= π×5×3 }$$

$$\mathrm{= 15π\: 或\: 47.12\: cm^2 }$$

結論

二維形狀具有長度、寬度或高度或半徑。要找到二維形狀（例如三角形、四邊形、多邊形、圓和橢圓）的面積，我們可以使用給定的測量值並應用公式。在三角形中，如果只給出兩條邊，我們可以使用勾股定理來找到另一條邊。圓和橢圓的面積是根據半徑測量的。

常見問題

1. 圓中的扇形是什麼？

當圓被分成幾部分時，它被稱為扇形，每個扇形包含兩條半徑和一條弧。每條弧都位於圓的圓周上。

2. 如何推匯出四邊形面積的公式？

考慮一個四邊形 PQRS，其對角線構成兩個三角形 ΔPQR & Δ RSQ。畫一條垂直線 PE 和 SF，這是三角形的高度。

$$\mathrm{四邊形的面積 = ΔPQR + ΔRSP}$$

$$\mathrm{面積 =\frac{1}{2}(對角線 × h_1) +\frac{1}{2}(對角線 × h_2) =\frac{1}{2} d( h_1+ h_2)}$$

3. 哪個公式可以應用於所有型別的三角形？

當給出三角形的邊長時，海倫公式可以應用於所有型別的三角形，例如不等邊三角形、銳角三角形和鈍角三角形。

4. 如何在多邊形中找到周長？

要找到任何多邊形（例如三角形、四邊形等）的周長，我們可以將所有邊加起來。

5. 面積的三維形式是什麼？

要找到二維物體所佔的空間，我們可以使用面積公式。面積的三維形式是三維形狀的體積。