梯形面積

---

簡介

梯形的面積是指梯形在二維平面中所覆蓋的區域。梯形是一個凸四邊形，只有一對平行邊。梯形是一個二維圖形。如果我們把它畫在紙上，它看起來像一張桌子。在歐幾里得幾何學的術語中，四邊形可以描述為恰好具有四條邊和四個頂點的多邊形。梯形的邊數、角數始終為四，且恆定不變。

現實世界中有很多梯形的例子。梯形的根本用途是梯形法則，它將曲線下的區域分成多個梯形，並計算每個梯形的面積。

梯形

平行四邊形也可以被稱為有兩條平行邊的梯形。

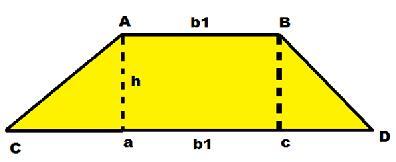
從上圖可以看出，AB邊和CD邊互相平行，而AC邊和BD邊是非平行邊。“h”表示兩條平行線之間的距離，代表梯形的高度。

梯形是一個封閉圖形或多邊形，其邊數、頂點數和角數都恰好為四。梯形中的一對平行邊也是其對邊。

在我們周圍有很多梯形的實際例子。

例如，帶有梯形表面的桌子。

梯形型別

梯形分為三種類型。這三種類型如下所示。

• 等腰梯形

• 不等邊梯形

• 直角梯形

不等邊梯形

所有邊長不相等梯形稱為不等邊梯形。

直角梯形

直角梯形至少有兩條相鄰的直角。一個直角梯形至少有一個直角。

不規則梯形

通常，當我們看到一個四邊形，其中一對邊平行，而另一對邊不相等但相等時，就可以識別出梯形。這些型別的梯形稱為規則梯形。對於不規則梯形，非平行邊不相等。這就是它們被稱為不規則梯形的原因。

梯形的性質

梯形的一些重要性質是：

• 在梯形中，只有一對平行邊，它們也是對邊。

• 對角線總是相交。

• 梯形的非等邊也非平行。除了等腰梯形外，它們不相等。

• 梯形的中位線等於平行邊之和的一半。

梯形的中位線

$\mathrm{中位線 =\frac{(AB+ CD )}{2}}$ 其中AB和CD是平行邊或底。

對於等腰梯形，腰或非平行邊是全等的。梯形的內角和等於360度，即

$$\mathrm{\angle A +\angle B +\angle C +\angle D = 360°}$$

兩個相鄰角的和是180°。這意味著兩個相鄰角互補。

梯形的面積

梯形的面積可以透過取梯形兩個底的平均值並乘以高來計算。因此，梯形法的面積由下式給出

$$\mathrm{梯形面積,\: A = \frac{h(a+b)}{2}\: 平方單位.}$$

其中“a”和“b”是底

“h”是高。

設等腰梯形ABCD的平行邊長分別為a和b。這相當於a是底邊長度，b是與a平行的邊長。c是兩條非平行邊的長度，h是等腰梯形的高度。其中

$$\mathrm{AB = a,\: CD = b,\: BC = AD = c}$$

當h垂直地從CD減去並與AB相交於E點時，就會形成一個直角三角形AED，垂直高度為

$$\mathrm{h = \sqrt{c^2 – (a-b)^2}[根據勾股定理]}$$

如你所知，梯形面積的公式為：

$$\mathrm{面積 =\frac{1}{2} h(a+b)}$$

$$\mathrm{等腰梯形面積 = \frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$$

例題

1)如果梯形的三個邊長分別為3、4、5，則梯形的面積是多少？

答：我們知道面積由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$給出。

因此，面積為

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{5^2 – (4-3)^2} (4+3)]= \frac{1}{2}\sqrt{24}(7)} \approx 17.08$$

因此，梯形的面積約為17.08。

2)如果梯形的三個邊長分別為5、6、7，則梯形的面積是多少？

答：我們知道面積由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$給出。

因此，面積為

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{7^2 – (6-5)^2} (5+6)]= \frac{1}{2} \sqrt{48}(11) } \approx 38.10$$

因此，梯形的面積約為38.10。

3)如果梯形的三個邊長分別為7、8、9，則梯形的面積是多少？

答：我們知道面積由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$給出。

因此，面積為

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{9^2 – (8-7)^2} (7+8)]= \frac{1}{2} \sqrt{80}(15) } \approx 67.08$$

因此，梯形的面積約為67.08。

4)如果梯形的三個邊長分別為10、11、12，則梯形的面積是多少？

答：我們知道面積由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$給出。

因此，面積為

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{12^2 – (11-10)^2} (11+10)]= \frac{1}{2} \sqrt{143}(21) } \approx 123.86$$

因此，梯形的面積約為123.86。

5)如果梯形的三個邊長分別為7、3、2，則梯形的面積是多少？

答：我們知道面積由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$給出。

因此，面積為

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{7^2 – (3-2)^2} (2+3)]= \frac{1}{2} \sqrt{48}(5) } \approx 17.32$$

因此，梯形的面積約為17.32。

結論

平行四邊形是具有兩對平行邊的四邊形。但是，梯形是隻有一對平行邊的四邊形。這些平行邊顯然位於相對位置。最大的平行邊通常被認為是梯形的底邊。

常見問題

1.梯形有平行邊嗎？

梯形是隻有一對平行邊的四邊形。這些平行邊顯然位於相對位置。

2.我們可以說梯形的對角線相等嗎？

梯形的對角線不必相等。梯形只有一對平行邊。但是，為了使四邊形具有相等的對角線，兩組線必須平行，例如正方形、矩形等。

3.在梯形中，對角線是否相交於彼此的中點？

梯形的對角線不相交於彼此的中點。如果對角線平分，梯形將變成平行四邊形。因此，所有平行四邊形都是梯形，但並非所有梯形都是平行四邊形。

4.正方形是梯形嗎？

是的，矩形必須至少有一對平行邊才能成為梯形，另外兩條線是否平行並不重要。

5.風箏是梯形嗎？

不是，風箏不是梯形，因為它沒有一對平行邊。