橢圓的面積

---

介紹

橢圓的面積是指橢圓在二維空間中所覆蓋的區域或面積。橢圓看起來像一個規則的卵形，當圓錐體被斜面截斷，且截面不與圓錐體的底面相交時，就會形成一個封閉的曲線，即橢圓。

橢圓是平面內到兩個定點距離之和為常數的點的軌跡。這兩個定點位於曲線內部，稱為焦點（單數：焦點）。這個常數的比值稱為橢圓的離心率，用字母'e'表示。這個定線稱為準線。

在我們的日常生活中，可以找到許多橢圓形的物體，例如板球場、羽毛球拍、行星軌道等等。在本教程中，我們將討論橢圓的面積。

橢圓

橢圓是圓錐曲線的一部分，具有與圓相似的特徵。與圓不同，橢圓具有卵形。橢圓的離心率小於1，表示到橢圓兩個焦點距離之和為常數的點的軌跡。

橢圓的特徵

• 有幾個特徵可以幫助我們從其他類似的形狀中識別出橢圓。這些橢圓的屬性如下：

• 當平面與圓錐體以其底角相交時，就會形成橢圓。

• 每個橢圓都有兩個焦點或焦距。橢圓上任意兩點到兩個焦點的距離之和為常數。

• 所有橢圓都有一箇中心，以及一個長軸和一個短軸。

• 所有橢圓的離心率都小於1。

橢圓的面積

橢圓的面積是指橢圓所覆蓋的二維面積或區域。橢圓是一個二維圖形，由連線平面上所有到兩個定點距離之和為常數的點形成。這兩個定點稱為橢圓的焦點。

橢圓的長軸是橢圓中最長的弦。垂直平分長軸的弦稱為短軸。

如果已知長軸和短軸的長度，則可以使用通用公式計算橢圓的面積。計算橢圓面積的公式如下：

$$\mathrm{橢圓面積 = π a b}$$

a = 半長軸長度

b = 半短軸長度

橢圓的通徑長度

通徑是一條穿過橢圓焦點的直線，並且垂直於水平軸。由於橢圓有兩個焦點，因此它有兩個通徑。

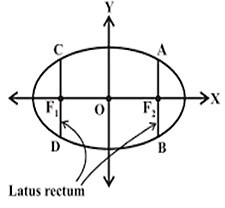
這是一個橢圓的圖形，其方程為

$$\mathrm{\frac{x^2}{a^2} +\frac{y^2}{b^2} =1}$$

其中 2a 是長軸的長度，2b 是短軸的長度。

CD 和 AB 是橢圓的通徑，點 A 的座標為 $\mathrm{(ae,\frac{b^2}{a})}$，點 B 的座標為 $\mathrm{(ae,-\frac{b^2}{a})}$，點 C 的座標為 $\mathrm{(-ae,\frac{b^2}{a})}$，點 D 的座標為 $\mathrm{(-ae,-\frac{b^2}{a})}$，其中 e 是橢圓的離心率。

因此，橢圓的通徑長度為

$$\mathrm{|\frac{b^2}{a}|+|\frac{b^2}{a}|=\frac{2b^2}{a}}$$

注意

• 平面內到兩個定點距離之和為常數的點的軌跡是橢圓。

• 橢圓面積 = π a b

• 將 π 的值視為 3.14 或 22/7

• 確定半長軸 (a) 和半短軸 (b) 的值，然後應用橢圓面積公式。

例題

1) 求長軸和短軸長度分別為 2 和 4 的橢圓的面積。

解答：我們知道，如果給出短軸和長軸的長度，則計算橢圓面積的公式為橢圓面積 = π a b。

$$\mathrm{橢圓面積 = π a b}$$

$$\mathrm{橢圓面積 = π ×2×4}$$

$$\mathrm{橢圓面積 = 8π }$$

2) 求長軸和短軸長度分別為 8 和 3 的橢圓的面積。

解答：我們知道，如果給出短軸和長軸的長度，則計算橢圓面積的公式為橢圓面積 = π a b。

$$\mathrm{橢圓面積 = π a b}$$

$$\mathrm{橢圓面積 = π ×8×3}$$

$$\mathrm{橢圓面積 = 24π }$$

3) 如果橢圓的方程為 $\mathrm{\frac{x^2}{16}+\frac{y^2}{144}=1}$，則求通徑的長度。

解答：已知橢圓的方程為 $\mathrm{\frac{x^2}{16}+\frac{y^2}{144}=1}$

$$\mathrm{\Rightarrow \frac{x^2}{4^2}+\frac{y^2}{12^2}=1}$$

現在將此方程與 $\mathrm{\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 進行比較

$$\mathrm{\Rightarrow a=4 and b=12}$$

我們知道通徑的長度為 $\mathrm{\frac{2b^2}{a}}$

因此，通徑的長度 = $\mathrm{\frac{2(12)^2}{4}=72}$

4) 如果橢圓的方程為 $\mathrm{\frac{x^2}{16}+\frac{y^2}{121}=1}$，則求通徑的長度。

解答：給定的方程為 $\mathrm{\frac{x^2}{16}+\frac{y^2}{121}=1}$

$$\mathrm{\Rightarrow \frac{x^2}{4^2} +\frac{y^2}{11^2} =1}$$

現在將此方程與 $\mathrm{\frac{x^2}{a^2}+\frac{y^2}{11^2}=1}$ 進行比較

$$\mathrm{\Rightarrow a=4\: and\: b=11}$$

我們知道通徑的長度 = $\mathrm{\frac{2b^2}{a}}$

因此，橢圓的通徑長度 $\mathrm{\frac{2(11)^2}{4}=\frac{121}{2}}$

5) 給定橢圓 $\mathrm{\frac{x^2}{16}+\frac{y^2}{25}=1}$ 的面積是多少？

解答：已知橢圓的方程為 $\mathrm{\frac{x^2}{16}+\frac{y^2}{25}=1}$

$$\mathrm{\Rightarrow \frac{x^2}{4^2}+\frac{y^2}{5^2}=1}$$

現在將此方程與 $\mathrm{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 進行比較

$$\mathrm{\Rightarrow a=4\: and\: b=5}$$

現在應用公式

$$\mathrm{橢圓面積 = π a b}$$

$$\mathrm{橢圓面積 = π ×4×5}$$

$$\mathrm{橢圓面積 = 20π }$$

結論

橢圓內部存在的區域數量定義為其面積。或者，橢圓的面積是可以放入其中的單位正方形的總數。

橢圓的面積是 π 與半長軸和半短軸長度的乘積。

常見問題

1. 橢圓的面積是什麼意思？

橢圓內部存在的區域數量定義為其面積。

2. 橢圓的通徑長度是多少？

橢圓的通徑長度為 $\mathrm{\frac{2b^2}{a}}$。

3. 通徑是什麼意思？

通徑是一條穿過圓錐曲線焦點的直線

並且平行於圓錐曲線的準線方向。

4. 什麼是橢圓？

與圓不同，橢圓具有卵形。橢圓的離心率小於1，表示到橢圓兩個焦點距離之和為常數的點的軌跡。

5. 橢圓面積的公式是什麼？

計算橢圓面積的公式如下：

$$\mathrm{橢圓面積 = π a b}$$

a = 半長軸長度

b = 半短軸長度