五邊形的面積

---

引言

五邊形的面積是指五邊形邊界所包圍的區域。具有五條直邊的多邊形稱為五邊形。大多數數學課堂作業都包括正五邊形，它有五條相等的邊。根據已知資訊量的多少，求面積通常有兩種方法。五邊形五條邊所包圍的區域稱為五邊形的面積。五邊形是一個只有兩個維度的五邊形。它的名稱來源於希臘語“Penta”（意為“五”）和“gon”（意為“角”）。在本教程中，我們將透過已解決的示例和練習題學習如何計算五邊形的面積。

五邊形

在幾何學中，五邊形是任何五邊形或五角形（源於希臘語 pente，意為五，gonia，意為角）。在一個簡單的五邊形中，內角之和為 540°。五邊形可以是簡單的，也可以是自相交的。五角星是一個自相交的正五邊形（有時稱為星形五邊形）。在下圖中，ABCDE 是一個不規則五邊形，FGHIJ 是一個正五邊形。

五邊形的面積

• 五邊形面積指的是五邊形各邊圍成的區域。根據已知尺寸的不同，可以使用不同的方法進行計算。

• 五邊形的型別也會影響計算方法。例如，如果是正五邊形，可以使用一個公式計算面積；但如果是負五邊形，則必須將其分割成多個多邊形，然後將它們的面積相加，才能得到五邊形的面積。

• 計算五邊形面積所用的公式取決於五邊形的型別。

• 常用的正五邊形面積公式是：

  $$五邊形面積 = \frac{1}{2}×pa$$

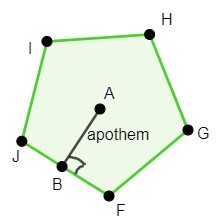
  這裡，“p”代表五邊形的周長，“a”代表其心距。在下圖中可以看到五邊形的心距“a”和邊長“s”。

例題

求邊長為 15 個單位，心距為 4 個單位的正五邊形的面積。

答案

已知 s=15 和心距=4

使用上述心距公式，我們可以計算正五邊形的面積如下：

$$五邊形面積 = \frac{1}{2}×pa$$

我們先計算周長：p=5s=5(15)=75 平方單位。

因此，

$$五邊形面積 = \frac{1}{2}×75×4=75×2=150 平方單位$$

• 如果只知道邊長“s”，也可以計算正五邊形的面積。計算正五邊形面積的公式為：$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$，其中 s 是正五邊形一邊的長度。

例題

求邊長為 5 個單位的五邊形的面積。

答案

已知：

s=5 個單位

因此，使用五邊形面積公式，我們得到：

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}} $$

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 5^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 25}=\frac{25}{4}\sqrt{5(5+2\sqrt{5})}\:平方單位} $$

• 不規則五邊形的面積可以透過將其分割成較小的多邊形來計算。然後計算每個多邊形的面積，並將它們加起來，得到五邊形的面積。

已解決的例子

1) 計算以下不規則五邊形的面積

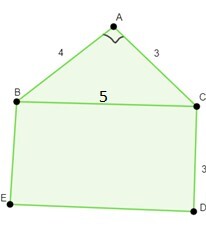
答案

注意，在五邊形 ABCDE 中，三角形 ABC 是一個直角三角形，四邊形 BEDC 是一個矩形。

因此，五邊形的面積是這兩個區域面積之和，即三角形 ABC 和矩形 BEDC 面積之和。

注意 $\mathrm{a(ΔABC)=\frac{1}{2}×底×高=\frac{1}{2}×3×4=6\: 平方單位}$

$$ \mathrm{a(BEDC)=3×BC=3×5=15\: 平方單位} $$

因此，五邊形 ABCDE 的面積為：

$$ \mathrm{a(ABCDE)=6+15=21\: 平方單位} $$

2) 求邊長為 8 個單位的五邊形的面積。

答案

已知：

s=8 個單位

因此，使用五邊形面積公式，我們得到：

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}} $$

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 8^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 64}=\frac{64}{4}\sqrt{5(5+2\sqrt{5})}\:平方單位} $$

3) 求邊長為 20 個單位，心距為 6 個單位的正五邊形的面積。

答案

已知 s=20 和心距=6

使用上述心距公式，我們可以計算正五邊形的面積如下：

五邊形面積 =$\mathrm{\frac{1}{2}×pa}$

我們先計算周長：p=5s=5(20)=100 個單位。

因此，

五邊形面積 =$\mathrm{\frac{1}{2}\times 100 \times 6=100\times 3=300\: 平方單位}$

4) 求邊長為 13 個單位，心距為 6 個單位的正五邊形的面積。

答案

已知 s=13 和心距=6

使用上述心距公式，我們可以計算正五邊形的面積如下：

五邊形面積 =$\mathrm{\frac{1}{2}×pa}$

我們先計算周長：p=5s=5(13)=65 個單位。

因此，

五邊形面積 =$\mathrm{\frac{1}{2}\times 65 \times 6=65 \times 3=195\: 平方單位}$

5) 計算邊長為 11 個單位的五邊形的面積。

答案

已知：

s=11 個單位

因此，使用五邊形面積公式，我們得到：

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}} $$

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 11^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 121}=\frac{121}{4}\sqrt{5(5+2\sqrt{5})}\:平方單位} $$

6) 計算邊長為 17 個單位的五邊形的面積。

答案

已知：

s=17 個單位

因此，使用五邊形面積公式，我們得到：

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}} $$

$$ \mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 17^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 289}=\frac{289}{4}\sqrt{5(5+2\sqrt{5})}\:平方單位} $$

結論

• 五邊形是一個有 5 條邊和 5 個角的多邊形。

• 它可以是正五邊形或不規則五邊形。

• 五邊形內角和為 540 度。

• 五邊形面積 =$\mathrm{\frac{1}{2}×pa}$（已知五邊形心距）。

• $\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$（已知正五邊形邊長）。

常見問題

1. 五邊形的所有角都相同嗎？

正五邊形有五條相等的邊和五個相等的角。因此，可以使用以下公式計算正五邊形的內角。

2. 五邊形有多少種不同型別？

五邊形是一種幾何圖形，具有五條邊和五個角。“Penta”代表五，“gon”代表角。五邊形是多邊形的一種。

3. 五邊形總是多邊形嗎？

五邊形有五條邊和五個角。它是一個多邊形。多邊形是具有封閉直邊和角的形狀。存在正多邊形和不規則多邊形，包括五邊形。

4. 五邊形有多少個角？

五邊形有五個內角。

5. 五邊形可能是凹的嗎？

五邊形和其他多邊形可以是凸的或凹的。如果五邊形或多邊形的所有內角都小於 180°，則它是凸的。如果一個或多個內角大於 180°，則它是凹的。凸五邊形總是正五邊形。

6. 五邊形可能是凸的嗎？

五邊形和其他多邊形可以是凸的或凹的。如果五邊形或多邊形的所有內角都小於 180°，則它是凸的。如果一個或多個內角大於 180°，則它是凹的。凸五邊形總是正五邊形。

7. 什麼是五邊形的心距？

心距是從五邊形的中心到一邊的線段，並且與該邊成 90 度直角。