心理學中正態機率分佈技術的應用
“正態”一詞的字面意思是平均。在心理學研究、社會學研究和教學中,那些在資格和特徵方面能夠達到特定固定水平的人被稱為正態。同時,那些高於或低於這個點的人是非正態的。大自然已經足夠慷慨地將大多數屬性(如體重、身高、智力等)分配得相當均勻。因此,我們大多數人擁有平均體重、身高、智力和此類屬性。相當一部分人明顯偏離平均水平,無論高於或低於。這同樣適用於從隨機選擇的樣本或人群中透過考試、調查和心理學、社會學和教育實驗收集的資訊,關於成績分數、智商分數、評分分數等。如果將這種分佈繪製在圖表紙上,就會形成一條有趣的典型曲線,類似於鐘形的垂直橫截面。這種鐘形曲線稱為正態曲線。
拉普拉斯和高斯(1777-1855)獨立推匯出了這條曲線。他們研究了物理學和天文學中的實驗誤差。他們發現結果誤差分佈是正態的——因此,誤差曲線被稱為正態誤差曲線或僅僅是誤差曲線。
什麼是正態機率分佈?
根據機率原理,它給出了連續變數的可能得分分佈。一位名叫亞伯拉罕·棣莫弗的數學家發展了這條曲線,它具有單邊的鐘形,具有雙側對稱性,並且建立在機率原理的基礎上。機率的根本原理建立在事件發生的可能性上,正態曲線描繪了這一原理。
計算
將連續變數得分(X)的頻率(f)繪製在一個相當大的樣本中觀察到的頻率,相對於其對應的得分(X),得到正態分佈曲線。
如果將相對頻率(fln)(透過將每個觀察到的頻率除以總頻率n獲得)繪製在其對應的標準分數(z分數)上,則可以得到類似形狀的分佈,這些標準分數是從原始X分數計算得出的,因為z分數是X分數的線性變換;然而,這種分佈被稱為正態分佈,因為它的Y縱座標提供了Z分數的相對頻率或機率,以及伴隨的X分數,而不是觀察到的頻率。
描述正態機率分佈的通用數學方程如下所示
$\mathrm{y = \frac{n}{\sigma\sqrt{2\Pi}}e^\frac{−x^{2}}{2\sigma^{2}}}$
其中,
$\mathrm{y}$ = 頻率
$\mathrm{n}$ = 觀察次數
$\mathrm{\sigma}$ = 分佈的標準差
$\mathrm{\Pi}$ = 3.1416(約)
$\mathrm{e}$ = 2.718(約),奈皮爾對數的底數
$\mathrm{x}$ = 測量值與平均值的偏差
示例
樣本量為1000例。測試分數的平均值為14.5,標準差為2.5。假設分佈為正態,計算12-16分數段中個體的數量。
解答
原始分數12和16都需要轉換為z分數。
原始分數12對應的z分數 = $\mathrm{\frac{X − M}{\sigma}}$
= (12−14.5)/2.5
= −2.5/2.5 = −1$\sigma$
原始分數16對應的z分數 = (16 − 14.5)/2.5 = 1.5/2.5
= 0.6 $\sigma$
根據正態曲線表,2257(10000中的),即22.57%的案例位於平均值和0.6 $\sigma$之間。類似地,在−1 $\sigma$和平均值之間,有3413,即34.13%的案例。這樣,可以很容易地得出結論,在1000人中,有22.57 + 34.13 = 56.7%或567人的分數在12-16範圍內。
性質
正態機率曲線是雙側對稱的。正態曲線圍繞稱為縱座標的垂直軸雙側對稱。50%的曲線位於最大中心縱座標的左側,另外50%位於右側。關於曲線中心點處的縱座標的對稱性表明,曲線一側的曲線斜率、形狀和大小與另一側相同。下圖顯示了中心中間點的左右兩半。
平均數 = 中位數 = 眾數
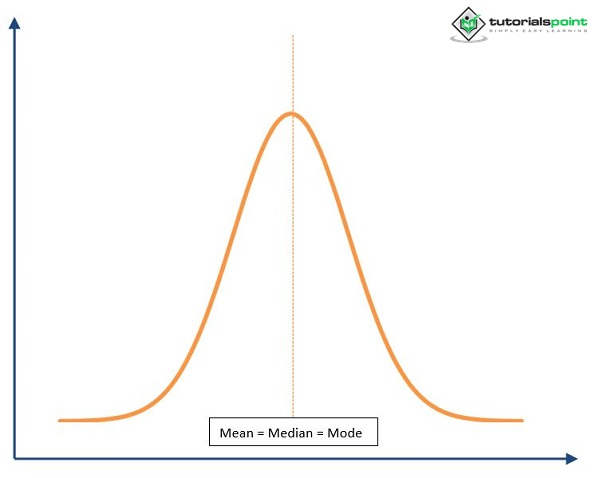
正態機率曲線是單峰的。曲線只有一個頂點,使其成為單峰的,並且只能有一個眾數。
最大縱座標位於中心附近。縱座標的高度始終在曲線的中心或中點達到峰值,在單位正態曲線上等於0.3989。
正態機率曲線漸近於X軸。曲線的高度在遠離中點兩端的逐漸減小,漸近地接近X軸,但永遠不會接觸X軸。因此,它的末端延伸到負無窮大($− \infty$)和正無窮大($+ \infty$)。
曲線高度均勻下降。從頂點向任一方向,曲線的高度都對稱下降。
拐點出現在±1個標準差($\pm \: 1 \: \sigma$)處。正態曲線方向從凸到凹的變化發生在一個稱為拐點的地方。從兩個拐點垂直繪製到X軸的線在平均值上下一個標準差單位的距離處接觸中心點。
正態曲線總面積在兩個拐點內的百分比是固定的。大約68.26%的總面積位於平均值±1個標準差($\pm$ 1 $\sigma$)單位的範圍內。
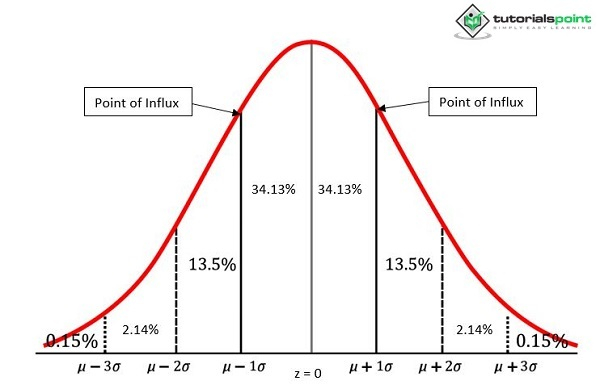
曲線覆蓋的總面積也可以接近100%的機率。曲線下的總面積可以認為接近100%的機率,用標準差來解釋。
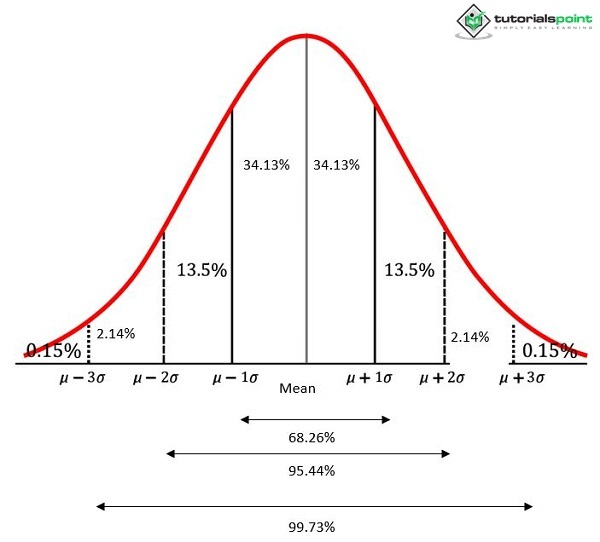
正態分佈中連續標準差之間護理的百分比。正態分佈作為峰度的基準。它具有中峰特徵——其峰度百分位係數為0.263。
正態性偏差
當測試分數的頻率分佈以直方圖或多邊形的方式圖形化地描繪時,人們很容易注意到曲線形狀的對稱性或不對稱性。三個引數——平均數、中位數和眾數——在正態曲線模型中重合;曲線的左右兩半完全平衡。通常,正態曲線中會出現兩種型別的偏差——峰度和偏度。
結論
正態機率曲線具有很重要的意義。它被廣泛應用於心理學、社會學和教育測量。它可以作為計算百分位數和百分位數排名、理解和應用標準測量誤差的概念以及轉換和組合定性資料的模型。正態機率分佈具有可以解決問題的應用,例如將原始分數轉換為z分數,並顯示正態曲線總面積相對於sigma距離的分數部分。


 資料結構
資料結構 網路
網路 關係型資料庫管理系統
關係型資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 語言程式設計
C 語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP